コンデンサーを用いた実験回路で微分積分の本質に迫る【微分編】:今岡通博の俺流!組み込み用語解説(14)(2/2 ページ)
微分の実験回路
ここまで幾つか事例を挙げた微分を電子回路で確かめてみましょう。図1は微分の動作を確かめる実験回路です。
コンデンサーと抵抗が用いられており、電子回路としてはCR微分回路として知られています。Cはコンデンサーで容量は47nF、Rは抵抗で抵抗値は560Ωです。
微分回路の特徴は、入力(IN)と出力(OUT)の間に直列にコンデンサーが挟まれていることです。そこで、2つの信号を同時に観測できる2現象オシロスコープを使って、入力側の波形と出力側の波形を比較することでコンデンサーによって引き起こされる微分現象を観測したいと思います。
さまざまな波形を使って微分現象を確かめる
今回の実験では、筆者が所持しているハンディーオシロスコープ「OWON HDS272S」を用いて観測します。このオシロにはシグナルジェネレーターの機能があり、これで生成した信号を入力信号とします。入力信号は1Vpp(波形の振幅の山から谷までの電位差が1V)で、周波数は1kHzです。
正弦波
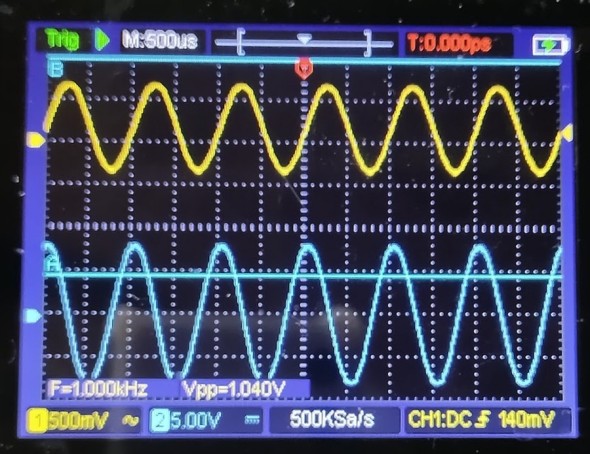
それではまずは正弦波の波形から見てみましょう。図2は入力波形と出力波形を比較するためのものです。
図2内の2つの波形のうち、上側の黄色い波形が入力信号で、下側の水色の波形が微分回路の出力波形です。出力波形の振幅が入力波形に比べて大きく映っていますがチャンネルごとに振幅のレンジが最適化されるのでこのようになっていますが、実際には出力波形の振幅の方がずっと小さくなっています。
それと、出力波形が入力波形に比べて少し横にずれているのを見て取れるでしょうか。サイン(sin)を微分するとコサイン(cos)になるという話を聞いたことないでしょうか。1波長は山から山あるいは谷から谷ですので、出力波形が1波長の4分の1分だけ時間軸上でずれるということなんですが、何かそれっぽい波形が出力されていませんか。学校で習った通りですね。こんな簡単な回路で複雑に見える微分の処理をちゃんとこなしているんですね。
矩形波
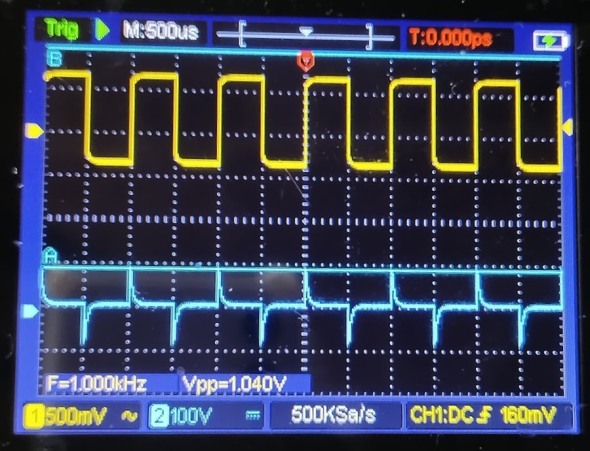
図3は矩形波の入力波形と、微分回路を通した後の出力波形を表示したものです。
矩形波とは一定間隔で2値の電圧を取る波形です。デジタル回路ではもっともよく見かける波形です。立ち上がりで正の方向に、立ち下がりで負の方向に変化します。
それでは図3下側の出力波形を見てみましょう。入力波形における立ち上がりと立ち下がりのタイミングで上下に鋭いスパイク状の波形になっているのが見て取れます。まず、入力波形の立ち上がりでは正の方向に急激に電圧が変化しますので、出力波形のその時点では正方向の鋭いスパイク状の波形になります。一方、入力波形の立ち下がりでは負の方向の鋭い波形となります。
いかがでしょうか、この図3でもちゃんと微分の仕事をしていますよね。
ノコギリ波
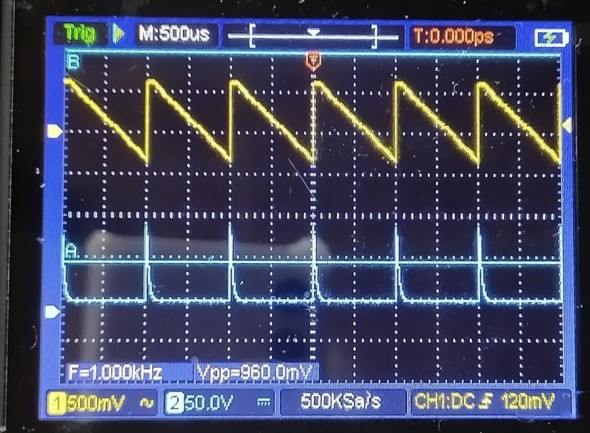
図4はノコギリ波を入力として、波形と微分回路を通した出力波形を映したものです。
ノコギリ波は、その昔ブラウン管でテレビを見ていたころ、画面走査の制御信号として利用されていました。最近だと、D級アンプや一部のA-Dコンバーターで使われていますね。
ノコギリ波の特徴は、ある時点で急激にある電圧値まで到達し、そこから一定のペースで電圧を下げて元の電圧に戻ります。この逆もあって、最初に一定間隔で電圧が上昇しある電圧値に達すると急激に元の電圧に下げるというものです。図4の上側に表示されている入力波形は前者ですね。
図4下側の出力波形を見ると、入力波形の立ち上がりのタイミングで鋭いスパイク状の波形が正方向に出ています。その後入力波形は一定間隔で電圧を徐々に下げていきますが、出力波形は一定の負電圧を示しています。
ここでも実験回路が立派に微分の仕事をしていますよね。
おわりに
いかがでしたでしょうか。これで少しは微分に対する苦手感は払拭(ふっしょく)できたでしょうか。微分の次は積分ということで、同様にコンデンサーを使った実験回路で解説したいと思います。お楽しみに。
関連記事
- ≫連載「今岡通博の俺流!組み込み用語解説」バックナンバー
- ≫連載「注目デバイスで組み込み開発をアップグレード」バックナンバー
 「コイル」は受動素子ナンバーワンの不思議ちゃん
「コイル」は受動素子ナンバーワンの不思議ちゃん
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第13回は、受動素子ナンバーワンの不思議ちゃんである「コイル」を紹介する。 オペアンプをコンパレーターとして使って見る
オペアンプをコンパレーターとして使って見る
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第12回は、オペアンプをコンパレーターとして活用する事例を紹介する。 組み込み技術者のためのコンデンサー活用術
組み込み技術者のためのコンデンサー活用術
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第11回は、組み込み技術者やデジタル技術者が知っておくとよいであろうコンデンサーの活用術を紹介する。 マイコンで機械式ロータリーエンコーダーを扱う
マイコンで機械式ロータリーエンコーダーを扱う
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第10回は、第7〜9回で取り上げたチャタリング対策を基に、回転動作をマイコンに伝えるデバイスとして広く使われている機械式エンコーダーとマイコンをつなぐプログラムを紹介する。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
- チップレットでASIL Dを支援する車載SoC技術を開発
- STPAの第4ステップで忘れがちな「損失シナリオ識別」の詳細手順
- 10BASE-T1S対応のPMDトランシーバー、CANのように簡便性とコスト低減を両立
コーナーリンク
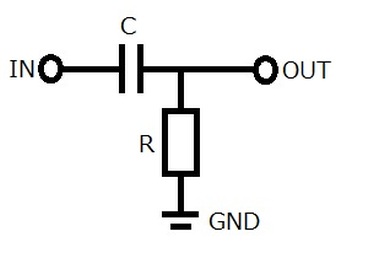 図1 微分の動作を確かめる実験回路
図1 微分の動作を確かめる実験回路