円筒座標系の熱伝導について考える:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(5)(2/4 ページ)
導体内部の温度分布
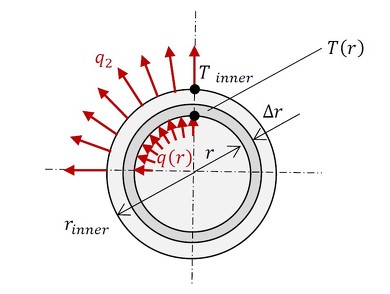
解析モデルを「円筒状の絶縁被覆とお考えください」と述べましたが、今度は導体を考えます。導体は図3で示した内側半径r1がゼロの中実円筒(円柱)と考えることができます。導体内部の温度分布の計算では、前項のr1がここでは外径に等しくなるため、外径をrinnerと表記します。図4に解析モデルを示します。
導体内部の温度分布を求めましょう。マイナスのrの世界へ熱は移動できないため、r=0での熱の流れはゼロとなり、次式が成立します(式10)。
熱流束は次式でした(式11)。
式11にr=0を代入すると都合が悪くなります。よって、中実円筒の場合はC1=0となります。
使うことのできる境界条件は、外周面の温度です。境界条件は以下です(式12)。
C1=0と上式を式9に代入します(式13)。
さらに、上式を式9に代入します(式14)。
Tinnerは次に述べる被覆内の計算結果を使います。
被覆内部の温度分布
微分方程式の解(式11)をそのまま使いますが、被覆内部では発熱はないとします。導体での全発熱量は式15で表されます。注意が必要なのは式15のAは導体側の単位体積当りの発生熱量です。
図3の内周面(r=r1)での熱流束は次式となります(式16)。
式16の関係を方程式の解である式11に代入します。式11のAは被覆側の発生熱量なのでゼロです。
被覆内部の熱流束は式18となります。
温度分布は次式となります(式19)。
境界条件を代入します。r=r1でT=T1、r=r2でT=T2ですね。
式20から式21を引き算しましょう。
上式は通過熱量と内周外周の温度差の関係式となり、参考文献[1]の式となりました。
次に、式20から式19を引き算します。
式24を式22で割り算しましょう。
式25も参考文献[1]に載っています。
熱伝達を含む伝熱計算は、主流の温度T∞が与えられ、熱伝達率を見積もって伝熱界面温度(この場合はT2)を求めるのが定石なので、式25ではなくT2を使った式を作ります。式21から式19を引き算します(式26)。
今度は式26を式22で割り算しましょう(式27)。
式27を式28のように変形します。
式28のT1−T2は式22の計算結果を代入することにし、被覆表面の温度T2は以下の式で求まります(式29、式30)。
参考文献:
- [1]日本機械学会|伝熱工学資料|改訂第4版|丸善(1999)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

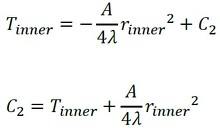 式13
式13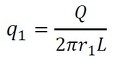 式16
式16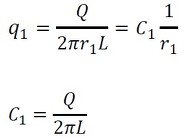 式17
式17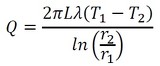 式23
式23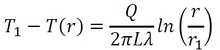 式24
式24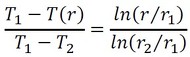 式25
式25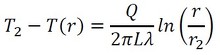 式26
式26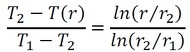 式27
式27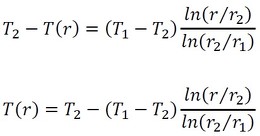 式28
式28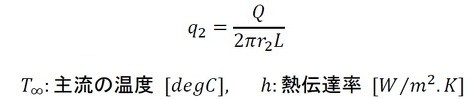 式30
式30





