円筒座標系の熱伝導について考える：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（5）（3/4 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

温度分布の数値例

　温度分布を計算して、CAE解析結果と比較しましょう。

　導体の発熱量と単位体積当たりの発熱量は次式で計算します（式31、式32）。

式31

式32

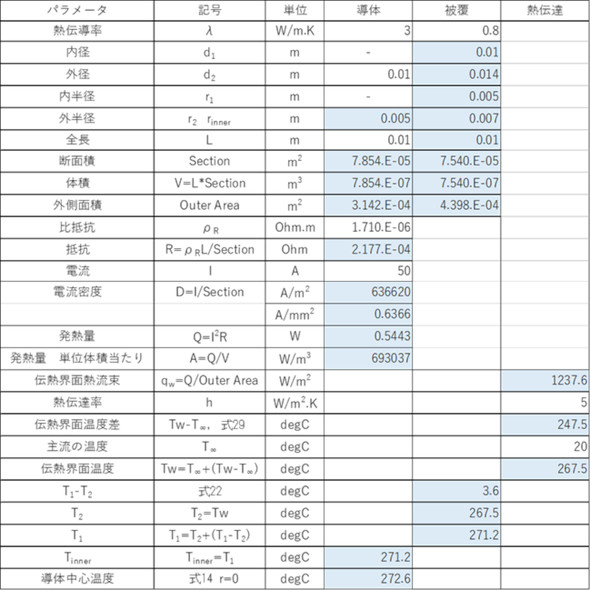
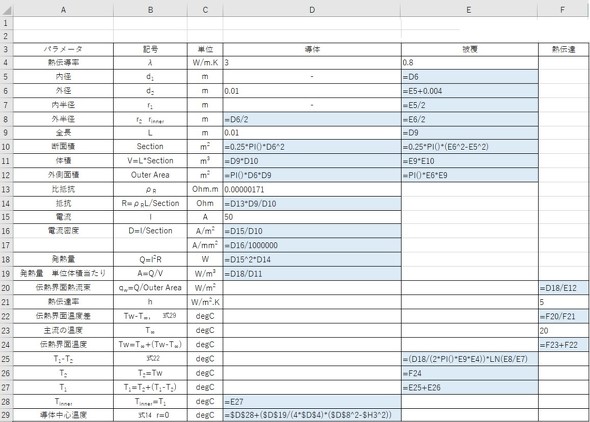
　表1と表2に数値代入例を示します。銅の熱伝導率は384［W/（m.K）］ですが、導体内部の温度分布を見るために、導体の熱伝導率を3［W/（m.K）］にしています。着色したセルには計算式が入っています。表1の値を「紙と鉛筆による計算結果」と呼びます。

表1　導体と被覆の温度［クリックで拡大］

表2　導体と被覆の温度：計算式［クリックで拡大］

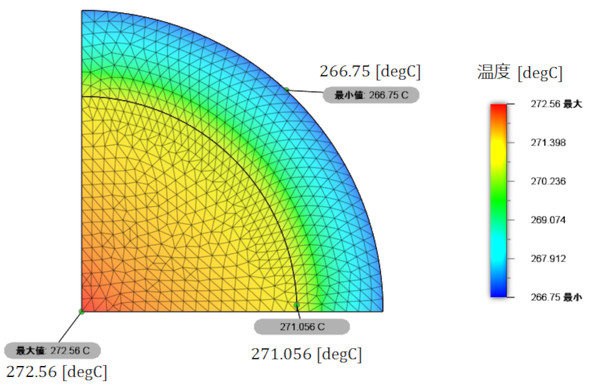
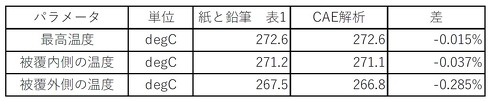
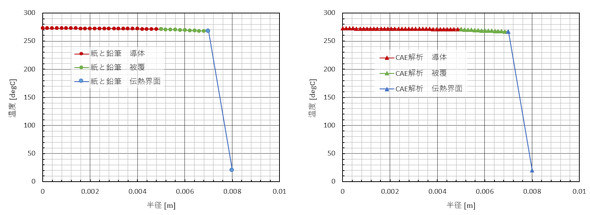
　図5にCAE解析結果を示します。表3に紙と鉛筆による計算結果とCAE解析結果の比較を示します。両者は一致しました。

図5　CAE解析結果［クリックで拡大］

表3　紙と鉛筆による計算結果とCAE解析結果の比較［クリックで拡大］

温度分布の考察

　図6に温度分布を示します。

図6　温度分布［クリックで拡大］

　図6左図の赤色プロット（紙と鉛筆 導体）は式14によるもので、緑色プロット（紙と鉛筆 被覆）は式28によるものです。両者が一致していることは分かりますが、導体内部の温度分布を詳しく見ましょう。

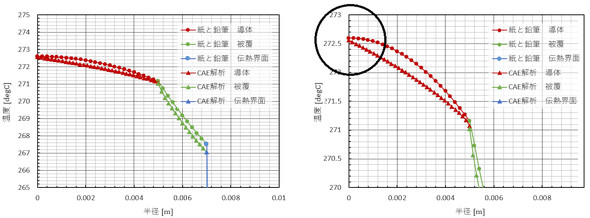
　図7に温度分布の拡大を示します。

図7　温度分布の拡大［クリックで拡大］

　図7右図の黒色○部の温度分布の傾きに注目します。「円筒座標系の半径座標rにマイナスはない」と述べました。つまり、半径がマイナスの世界に熱は伝わりません。半径方向熱流束はゼロなのです。この結果、フーリエの法則から温度勾配はゼロで、グラフの傾きは水平になるはずです。しかし、CAE解析結果のグラフの傾きはゼロになっていません。

　紙と鉛筆、CAE解析の双方における導体中心温度（最高温度）に違いはないので、特に問題視することではありませんが、「この筆者、また細かいこと言ってるよな〜」と思われそうです。