機械設計の基礎はアナログに詰まっている 〜JIS製図法(その3)〜:若手エンジニアのための機械設計入門(3)(2/2 ページ)
なぜ幾何公差なのか 〜図面の曖昧さをなくす〜
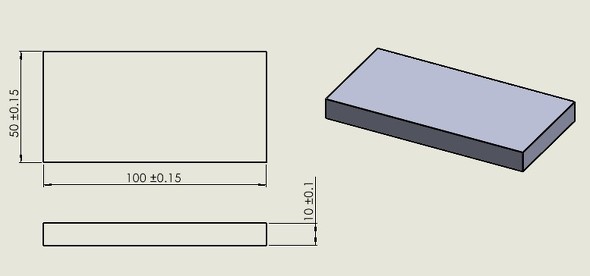
幾何公差の目的は何でしょうか。図3はサイズ公差のみで描かれた図面です。ご覧の通り、“相対する平行2平面のサイズ”とその“サイズ公差”によって指示されています。
この形状を頭の中で思い浮かべたとき、日本では誰もが完全な直方体をイメージします。6面が垂直、対面が平行となる直方体の形態であり、そのサイズも100±0.15[mm]、50±0.15[mm]、25±0.1[mm]の範囲に入り、それぞれの面も平面度が確保されている部品として加工されることを期待します。
しかし、この図面は厳密にいうと「6面が垂直ではなく、断面形状がひし形になっていたとしても、各角サイズ公差を満足していれば問題ない」と解釈することもできます。
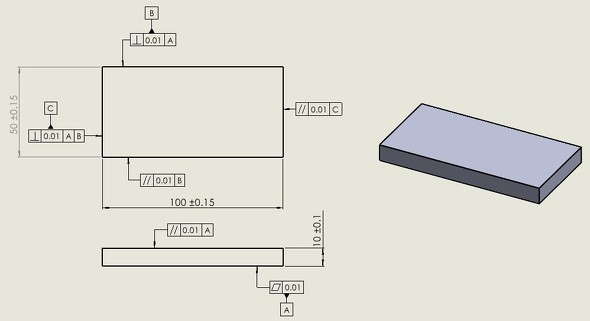
そこで以下の考えに従い、図4のような図面を描いてみました。
- 直方体モデルの平面(下面)がデータムA。このデータムAは0.01以内の平面によって構成されている。これに相対する面は平行度0.01以内とし、サイズ公差によって9.9〜10.1mmまで許容する
- 短手(みじかて)方向は、データムAに対して垂直度0.01以内の面をデータムBとし、その相対する面の平行度は0.01以内。この2面間のサイズは49.85〜50.15mmまでを許容する
- 長手方向は、第1にデータムA、第2にデータムBに対して垂直度0.01以内にある面をデータムCとし、相対する面はデータムCに対して平行度0.01以内。この2面間のサイズは99.85〜100.15mmまでを許容する
サイズ公差と幾何公差を別々に考えることを「独立の原則」といいます。独立の原則は、JISに次のように記載されています。
JIS B0024-1988(ISO 8015-1985) ※抜粋/編集「独立の原則」
図面上に個々に指定した寸法および幾何特性に対する要求事項は、それらの間に特別の関係が指定されない限り、独立に適用する。それ故、何も関係が指定されていない場合には、幾何公差は形体の寸法に無関係に適用し、幾何公差と寸法公差は関係のないものとして扱う。
- 寸法と形状または
- 寸法と姿勢または
- 寸法と位置
との間に特別な関係が要求される場合には、そのことを図面上に指定しなければならない。
幾何公差によって、サイズ公差だけでは曖昧だった形体の公差領域がさらに明確に制約され、形体がより詳細に示されるようになります。つまり、図面の曖昧さがなくなり、誰もが図面から同じ解釈ができるようになることで、“図面の一義性”が向上します。
なお、図4の記入方法に関しては、以下の妥当性評価が必要となります。
- この部品を含む組み立てがどうなっているか
- 幾何公差を指示した形体がどのような目的で使用されているか
一般公差/普通公差
前述の通り、サイズ公差と幾何公差によって図面の曖昧さを抑えることができます。ここでは、さらにその理解を深めていくために「一般公差」について紹介します。
一般公差とは、図面上で明示的に公差が指定されていない寸法に適用される標準的な許容範囲のことです。一般公差は「普通公差」とも呼ばれています。
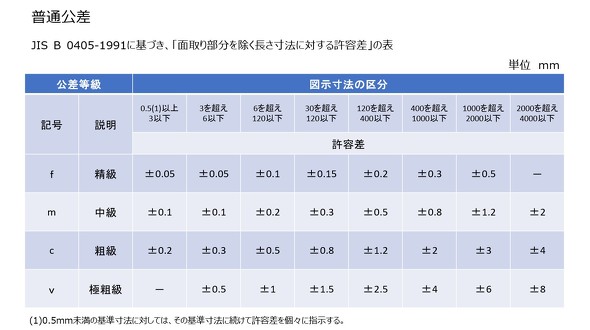
そして、この一般公差の定義については「JIS B 0405-1991(ISO 2768-1:1989)普通公差-第1部:個々に公差の指示がない長さ寸法及び角度寸法に対する公差 General tolerances - Part 1:Tolerances for linear and angular dimensions without individual tolerance indications」に示されています。
設計者が個々の寸法に対して公差を指定する手間を省き、見やすい図面を描くために使用されています。
筆者の経験では、一般的な構造物を構成する部品加工のための「中級」を使用することがほとんどでしたが、部品の用途によっては「精級」を使用することもありました。この場合、当然ですが加工コストも上がります。また、企業ごとに標準幾何公差として何を使用するかを定めていることが一般的です。
次回も幾何公差の解説を続けます。 (次回へ続く)
関連記事
 データムを必要とする幾何公差【その1】〜姿勢公差の平行度〜
データムを必要とする幾何公差【その1】〜姿勢公差の平行度〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第8回はデータムを必要とする幾何公差をテーマに、姿勢公差の平行度について取り上げる。 データムを必要とする幾何公差【その2】〜姿勢公差の直角度〜
データムを必要とする幾何公差【その2】〜姿勢公差の直角度〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第9回はデータムを必要とする幾何公差をテーマに、姿勢公差の直角度について取り上げる。 データムを必要とする幾何公差【その3】〜姿勢公差の傾斜度〜
データムを必要とする幾何公差【その3】〜姿勢公差の傾斜度〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第10回はデータムを必要とする幾何公差をテーマに、姿勢公差の傾斜度について取り上げる。 データムを必要とする幾何公差【その5】〜位置公差の位置度〜
データムを必要とする幾何公差【その5】〜位置公差の位置度〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第12回は「位置公差」のうち「位置度」について取り上げる。 位置度を考える上で重要な「最大実体公差」の「動的公差線図」
位置度を考える上で重要な「最大実体公差」の「動的公差線図」
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第14回は、位置度を考える上で重要な最大実体公差の「動的公差線図」について取り上げる。 位置公差の総仕上げと振れ公差について 〜曖昧さを取り除く幾何公差〜
位置公差の総仕上げと振れ公差について 〜曖昧さを取り除く幾何公差〜
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。最終回となる第15回は「位置公差」の残りと「振れ公差」について取り上げ、幾何公差の解説をまとめます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞