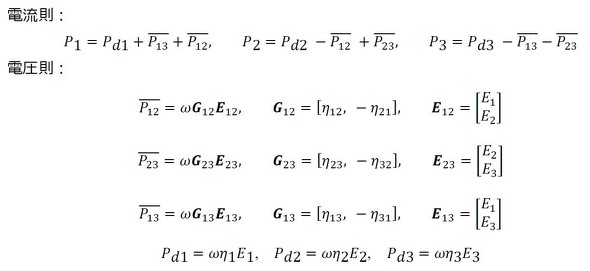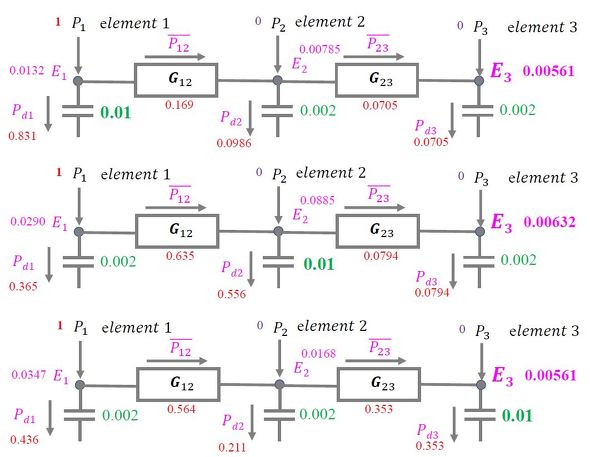
　本方法の設計応用はさまざま考えられる。図2下図（板1にパワーを入力）の例では、板3のエネルギーがE₃＝0.0167［J］であった。そこで、この値をE₃＜0.01［J］となるように設計することを考える。そのためには、板から板へのパワーの伝わり方を小さくすればよい。結合損失係数の定義から結合長さを大きくすればよいことが分かる。

　ただし、この方法では構造物の形状自体を変更しなければならず、他への影響が大きい。そこで、構造は変更せずに、板自体の内部損失係数を大きくすることを考える。現状はη＝0.002としている。この値は、構造材料自体が有している損失係数を想定している。そこで、減衰パネルなどを付加することにより、η＝0.01とすることを考える。

　このとき、付加する減衰パネルは十分に薄く、軽く、柔らかく、母体材料（この場合は鉄）に比べて、ヤング率、密度は無視できるレベルとする。また、3枚の板全てに減衰パネルを貼ってもいいが、コストの問題もあるので、効果的と思われる板1枚にのみ貼ることにする。

　図3に、減衰パネルを貼る位置を、板1、板2、板3と変えた場合の結果を示す。

図3　各板の内部損失係数を変えた場合の結果［クリックで拡大］

　この結果、いずれの場合も目標のE₃＜0.01［J］を達成できていることが分かる。ただし、その効果は微妙に異なり、板1または板3に貼った場合が最も板3の振動エネルギーが小さくなる。

　板1に貼った場合、板3だけでなく、板1、板2の振動エネルギーも小さくできるので最も良い設計といえる。対象とする部位に対策を施すのもよいが、振動発生源（この場合は板1）に対策を行うのが最も効果的であるという“振動対策の鉄則”を示しているといえる。

音振動連成問題：定式化

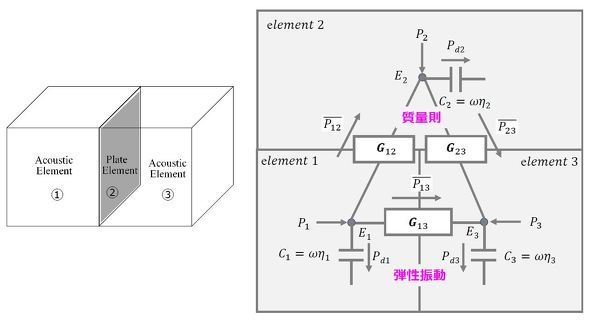
　音響振動連成問題への適用例として、図4左図に示す2つの部屋（音場）が板を介して結合された構造を考える。

図4　2つの部屋（音場）が板を介して結合した構造［クリックで拡大］

　例えば、音場1で音を発生させた場合、板を介して、音響エネルギーが音場3に伝わる。板は音に関して遮音効果を有しており、音場1から音場3に音が伝わる際、板の質量効果によって音が減衰するとともに、板の弾性振動によってある周波数で遮音効果が劣化するコインシデンス効果があることが知られている。そこで、質量則とコインシデンス効果を評価するために、図4左図を図4右図のようにモデル表現する（参考文献［1］）。

　図4のフロー図を基に、電流則、電圧則を適用すると次式となる。

式4［クリックで拡大］

　上式には、次の9つの未知数に対する、9つの式があるので解くことができる。

9つの未知数

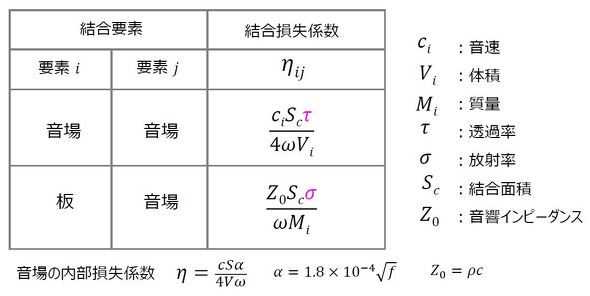
　この場合の音場間および板と音場間の結合損失係数を表1に示す。透過率τに質量則の効果が、放射率σに板の弾性振動の影響が考慮されている。詳しい導出式については参考文献［2］を参照してほしい。

表1　音場間および板と音場間の結合損失係数［クリックで拡大］

参考文献：

［1］Crocker, M. J., and Price, A. J.｜Sound transmission using statistical energy analysis｜Journal of Sound and Vibration｜Vol.9 No.3（1969）
［2］入江良彦｜SEA法による固体伝搬音解析｜日本音響学会誌 48巻6号（1992）

音振動連成問題：解析例

前のページへ 1|2|3 次のページへ