フローで考える音振動のモデリング(その2) 〜振動問題、音振動連成問題に適用する〜:1Dモデリングの勘所(35)(1/3 ページ)
「1Dモデリング」に関する連載。連載第35回では「フローで考える音振動のモデリング(その2)」と題し、振動問題、音振動連成問題に適用する際の定式化の方法などについて解説する。
前回、音振動問題をエネルギー問題に置き換える“フローで考える音振動のモデリング”の理論的背景と、1Dモデリングへの拡張方法を説明した。今回は、これを振動問題ならびに音振動連成問題に適用する際の定式化の方法、解析例、そして設計応用の事例について述べる。
振動問題:定式化
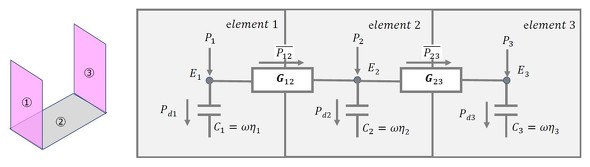
図1左図に示す3つの板が直角に結合した構造物の振動問題を考える。この3つの板をエネルギー(パワー)フローで考えてモデル図にすると図1右図のようになる。
図1のフロー図を基に、熱、流れの場合と同様に電流則、電圧則を適用すると次式となる。
上式について、対象とする周波数ωを決め、板の物性(ヤング率、ポアソン比、板厚、密度、損失係数)を設定して、パワーの入力点とその大きさを指定し、結合損失係数を定義して解くことにより、各板の振動エネルギー、各フローの振動パワーを求めることができる。上式には、次の8つの未知数に対する、8つの式があるので解くことができる。
板間の結合損失係数ηijは、前回の表2より求まる。すなわち、
となり、Cgiは板の曲げ波の群速度で次式によって定義される。
また、Siは板の面積、Lcは板と板の結合長さ、τは板から板への透過率であり、前回の図6で示すように定義される。図1の例は、各板が直角に結合されているので板厚が同じ場合は、透過率はいずれも0.5となる。
振動問題:解析例
以上の知見を基に、式を「Modelica」でテキスト表記すると以下のようになる(リスト1)。ここでは、3つの板はいずれも各辺1mの矩形(くけい)板とし、対象とする周波数を1000Hzとした。また、結合損失係数は、板材料を鉄とし、ヤング率を2.1×1011[Pa]、損失係数を0.002、ポアソン比を0.28、密度を7830[kg/m3]、板厚を0.001mとして別途計算した結果、すなわち、ηij=5.01e-3を用いている。
model energy3plates import Modelica.Constants.pi; Real Pd1 “internal loss power of plate1”; Real Pd2 “internal loss power of plate2”; Real Pd3 “internal loss power of plate3”; Real P12 “power from plate1 to plate2”; Real P23 “power from plate2 to plate3”; Real E1 “energy of plate1”; Real E2 “energy of plate2”; Real E3 “energy of plate3”; Real C1 “internal loss factor of plate1”; Real C2 “internal loss factor of plate2”; Real C3 “internal loss factor of plate3”; Real omg “target angular frequency”; parameter Real P1=0 “input power to plate1” ; parameter Real P2=1 “input power to plate2”; parameter Real P3=0 “input power to plate3”; parameter Real freq=1000 “target frequency Hz”; parameter Real ita1=0.002 “internal loss coefficient of plate1”; parameter Real ita2=0.002 “internal loss coefficient of plate2”; parameter Real ita3=0.002 “internal loss coefficient of plate3”; parameter Real ita12=5.01e-3 “coupling loss factor from plate1 to 2”; parameter Real ita21=5.01e-3 “coupling loss factor from plate2 to 1”; parameter Real ita23=5.01e-3 “coupling loss factor from plate2 to 3”; parameter Real ita32=5.01e-3 “coupling loss factor from plate3 to 2; equation C1=omg*ita1; C2=omg*ita2; C3=omg*ita3; omg=2*pi*freq; Pd1=C1*E1; Pd2=C2*E2; Pd3=C3*E3; P12=omg*(ita12*E1-ita21*E2); P23=omg*(ita23*E2-ita32*E3); P1=Pd1+P12; P2=Pd2-P12+P23; P3=Pd3-P23; end energy3plates;
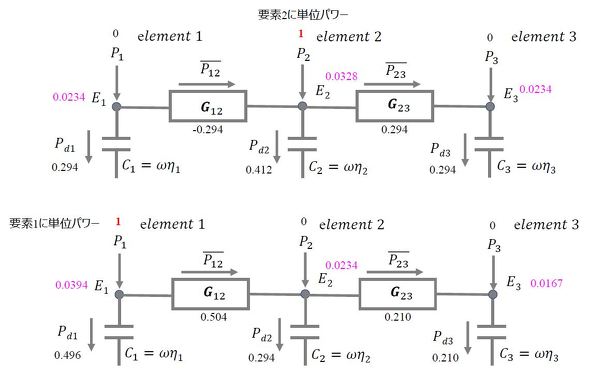
図2に解析例を示す。図2上図は板2に単位パワーを入力した場合、図2下図は板1に単位パワーを入力した場合の結果である。
図2上図では、真ん中の板にパワーを入力しているので、板1および板3へのパワーの流れは対称で、板1および板3の振動エネルギーも同じになっている。エネルギーはスカラ量であるが、パワーは方向を持っているので、図中でパワーが(−)ということは、図のパワーの矢印方向と逆方向にパワーが流れていることを意味する。
図2下図では、板1にパワーを入力しているので、板1→板2→板3とパワーが減衰しながら流れ、その結果として、各板の振動エネルギーはE1>E2>E3となっている。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
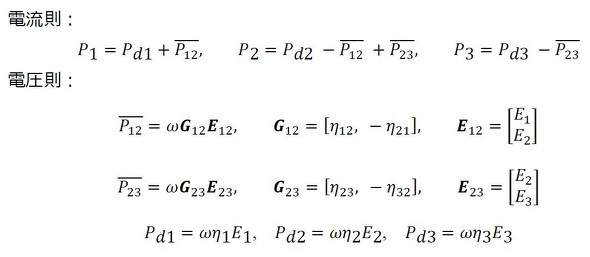
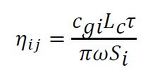 式2
式2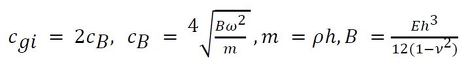 式3
式3