溶接部の疲労強度(その1):CAEを正しく使い疲労強度計算と有機的につなげる(10)(4/5 ページ)
CAE解析を使った溶接部の疲労強度評価
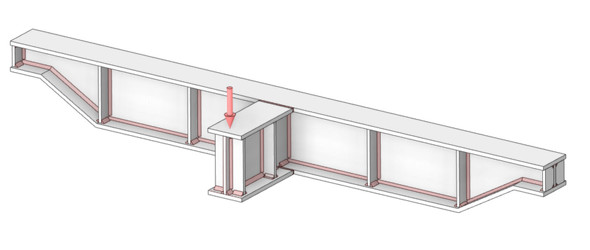
図12に溶接構造物を示します。図のような荷重が作用したときの溶接ビードのルート断面の公称応力や溶接止端部のホットスポット応力を求めたい場合、手計算では困難であるため、有限要素法の出番となります。
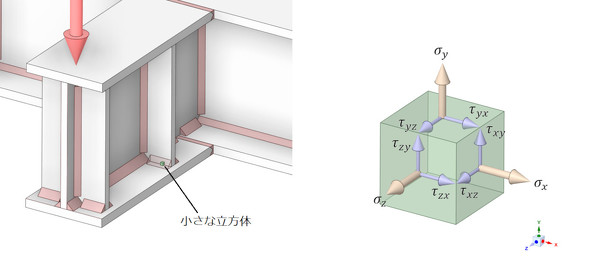
図13に溶接ビードの中の小さな立方体と、それに作用する応力を示します。溶接ビードには、のど断面に垂直な応力しか作用していないことはあり得ず、6種類の応力が作用しています。図では応力は9つありますが、τxy=τyxなので、応力は6成分となります。このような場合はどうするのでしょうか。
6成分の応力が作用しているときは、公称応力で表した主応力で強度評価するとの記載が参考文献[1]にあります。それに従いましょう。CAE解析では図2に示したように、応力集中部の応力が求まりますが、公称応力は求まりません。どうしましょうか。簡単な例を使って、公称応力で表した主応力をCAE解析で求めることができるか確認してみましょう。
参考文献:
- [1]日本鋼構造協会|鋼構造物の疲労設計指針・同解説|技報堂出版(2014)
CAE解析を使った溶接部の公称応力の求め方
以下に、この章のあらすじを示します。
- のど断面の公称応力として、CAE解析で求めたのど断面の第一主応力の平均値を提案する
- 簡単な例を使って、手計算で求めたのど断面の公称応力とCAE解析によるのど断面の第一主応力の平均値を比較する
- 両者が近い値であることを示す
- 止端部の公称応力として、CAE解析で求めたホットスポット応力を提案する
- 簡単な例を使って、手計算で求めた止端部の公称応力とCAE解析によるホットスポット応力を比較する
- 両者が近い値であることを示す
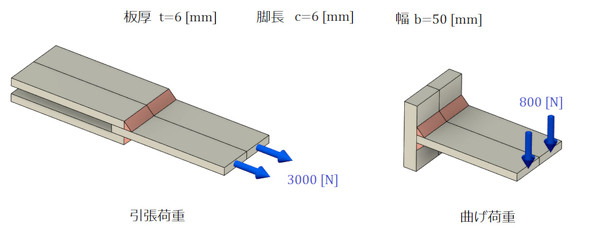
図14のようなすみ肉溶接の手計算による応力と、CAE解析による主応力を比較してみましょう。板の中央に線が入っているのはホットスポット応力を求めるためです。
図14左図の引張荷重の例では、のど断面応力は次式となります。
図15に、CAE解析結果を示します。ここからのど断面の応力を抽出するのは少し骨が折れますが図16のようになり、応力値をテキストファイルで出力して「Excel」で平均値を求めました。のど部断面の第一主応力の平均値は6.6[MPa]となりました。
次は止端部応力です。公称応力は以下となります。
文献でも述べられているように、CAE解析による方法では止端部応力(公称応力)はホットスポット応力で代用します。図15のA線上の応力をテキストファイルとして出力し、Excelに取り込みます。これを図17に示します。
止端部では、強烈な応力集中が発生しています。板厚の0.5倍の応力と1.5倍の応力から直線を引いて止端部の応力を求めるのですが、0.5倍の応力が少しへこんでいます。これは無視しましょう。ホットスポット応力は10[MPa]ですね。
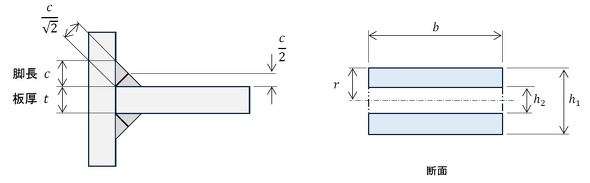
図15右図の曲げ荷重の例はどうしましょうか。文献にはありませんが、のど断面応力についてははりの曲げ理論を使いましょう。図18に断面二次モーメントを求めるための断面を示します。溶接ビードをはりの断面と考える発想です。
曲げ応力は、次の式16で求まります。
r寸法を求めるところで意見が分かれると思います。以下のようなものがあるでしょうか。
はりの曲げ問題の場合、断面の最大応力を求めるため、式17を使うことになりますが、ここで求めたいのは平均応力です。こうなると式18か式19となりますが、曲げ応力が大きい方の式18を使いましょう。曲げ応力は以下となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

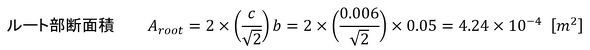 式12
式12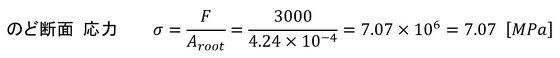 式13
式13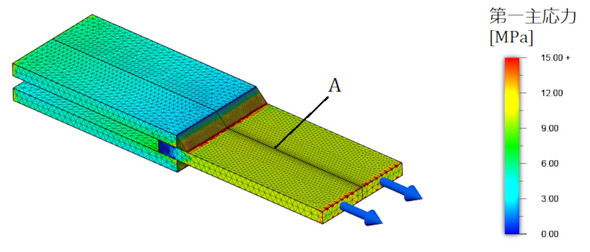
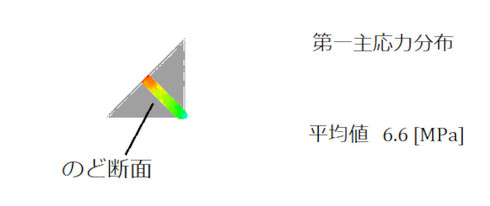
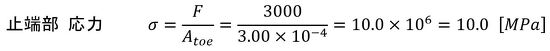 式15
式15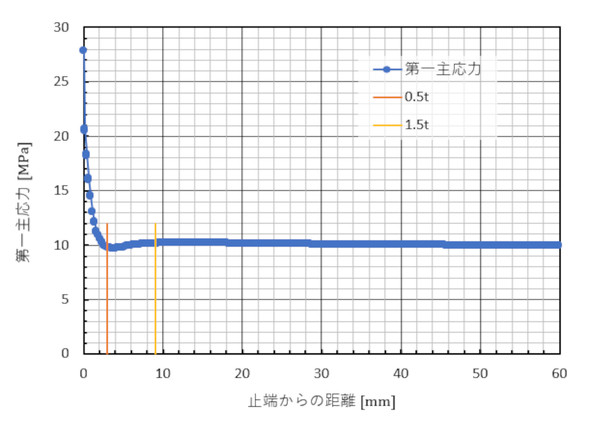
 式16
式16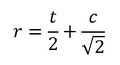 式17
式17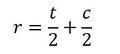 式18
式18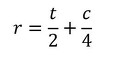 式19
式19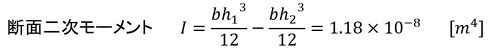 式20
式20





