フローで考える熱のモデリング(その2) 〜熱コンダクタンスの定義と導出方法〜:1Dモデリングの勘所(32)(4/5 ページ)
» 2024年06月13日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
対流熱伝達に関する熱コンダクタンス
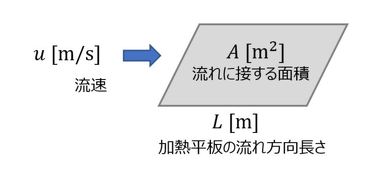
以上の知見を基に、加熱平板の対流熱伝達に関する熱コンダクタンスを求める。最初に、図8に示す強制対流熱伝達について考える。
強制対流熱伝達は一般に、
で表現できる。すなわち、加熱面が外部からの流れを受ける場合の熱伝達である。水平平板の強制対流層流平均熱伝達は、
で、強制対流乱流平均熱伝達は、
で表現可能であることを、いくつかの仮定の下に導出できる(参考文献[1])。ここで重要なのは、乱流の方が層流に比べてその攪拌作用によって熱伝達が大きいということだ。
上記式に、具体的に数値を代入してそうであることを確認してみる。流速u=10[m/s]、平板大きさ0.1×0.1mとすると、層流に関して、
model forcedHeatTransferLam import Modelica.Constants.pi; Real Pr; Real Re; Real G; Real h; Real mu; parameter Real ram=0.03; parameter Real c=1000; parameter Real nu=15e-6; parameter Real A=0.01; parameter Real L=0.1; parameter Real ro=1; parameter Real v=10; equation Pr=mu*c/ram; Re=v*L/nu; h*L/ram=0.664*Pr^(1/3)*Re^(1/2); G=h*A; mu=ro*nu; end forcedHeatTransferLam;
リスト1
となり、乱流に関しては、
model forcedHeatTransferRan import Modelica.Constants.pi; Real Pr; Real Re; Real G; Real h; Real mu; parameter Real ram=0.03; parameter Real c=1000; parameter Real nu=15e-6; parameter Real A=0.01; parameter Real L=0.1; parameter Real ro=1; parameter Real v=10; equation Pr=mu*c/ram; Re=v*L/nu; h*L/ram=0.037*Pr^(1/3)*Re^(4/5); G=h*A; mu=ro*nu; end forcedHeatTransferRan;
リスト2
となる。上記を実行すると、
- 層流熱伝達に関する熱コンダクタンス:G=0.408[W/K]
- 乱流熱伝達に関する熱コンダクタンス:G=0.637[W/K]
となる。この結果は、熱伝達率でいうと層流で40.8、乱流で63.7であるため、前回の図8の“熱伝達率の目安”の媒体が空気の場合の強制対流の値に合致している。
続いて、自然対流熱伝達について考える。自然対流熱伝達は一般に、
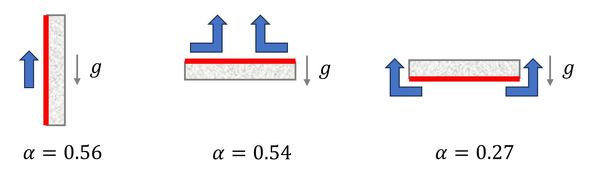
で表現される。加熱平板の場合、β=1/4、γ=1/4、また平板の設置方向によってαは図9に示す値となることが経験的に分かっている(参考文献[2])。
強制対流熱伝達と同じ加熱平板を垂直に設置し、平板表面温度を80℃、雰囲気温度を15℃とすると、
model naturalHeatTransfer import Modelica.Constants.pi; import Modelica.Constants.g_n; Real Pr; Real Gr; Real G; Real h; Real mu; Real beta; parameter Real ram=0.03; parameter Real c=1000; parameter Real nu=15e-6; parameter Real A=0.01; parameter Real L=0.1; parameter Real ro=1; parameter Real Alfa=0.56; parameter Real Ts=80; parameter Real Ta=15; equation Pr=mu*c/ram; Gr=beta*g_n*(Ts-Ta)*L^3/nu^2; beta=1/(Ts+273.15); h*L/ram=Alfa*Gr^(1/4)*Pr^(1/4); G=h*A; mu=ro*nu; end naturalHeatTransfer;
リスト3
となり、これを実行してG=0.075[W/K]を得る。この結果は、熱伝達率でいう7.5であるので、前回の図8の“熱伝達率の目安”の媒体が空気の場合の自然対流の値に合致している。
参考文献:
- [1]庄司正弘|伝熱工学 8.1節、8.2節|東京大学出版会(1995)
- [2]JSMEテキストシリーズ|伝熱工学 3.7節(2005)
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
Special SitePR
あなたにおすすめの記事PR