フローで考える熱のモデリング(その2) 〜熱コンダクタンスの定義と導出方法〜:1Dモデリングの勘所(32)(2/5 ページ)
強制対流熱伝達
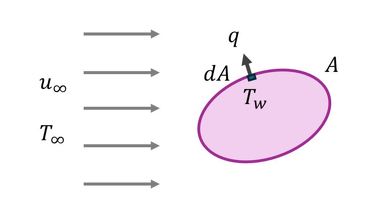
図4に示すように、高温の物体(表面温度一定のTw)の周りに低温の流体(温度T∞)が流れている場合を考える。
このとき、物体表面からの熱流束は、
となる。熱伝達率hは場所によって異なり、物体全表面からの熱量は、
となる。物体表面の平均熱流束を
と定義すると、
となり、hmを「平均熱伝達率」、最初の式のhを「局所熱伝達率」という。熱伝達率は、熱伝導率、温度伝導率と異なり、流体の物性だけで決定することはできず、以降で述べるように、物体の形状や流れの状態によって決まる。
平板に沿った流れを考えると、図5に示すように先端位置に近い部分は層流、下流では乱流となる。
層流境界層内の流れは粘性に支配されていて、流速分布に対応したせん断応力τが流れ方向に作用する。その大きさは、
となる。平板表面のせん断応力τwは式16となる。
平板表面では、流体の分子は平板の表面に固定されている(静止している)ので、平板表面からの熱流束は熱伝導の基本式から、
となる。式17と前述の熱伝達の基本式から、
となる。すなわち、熱伝達率は温度境界層の温度勾配によって決まる。層流は乱流に比べて平板表面の温度勾配が小さいため、図5上図に示すような熱伝達率となる。
熱伝達率の評価には、境界層内の熱と流れが関係する。そこで、図6の座標系で、熱と流れの支配方程式を境界層近似すると下記となる。
上式の各変数を
により無次元化すると以下となる。
Reを「レイノルズ数」といい、
をプラントル数と呼ぶ。
一方、物体表面の熱伝達率は、
となる。これから、熱伝達に関する無次元数である「ヌッセルト数」を以下のように定義する。
ヌッセルト数は温度で決まるので、前述の運動方程式の無次元数であるレイノルズ数、プラントル数で表現できる。すなわち、
となる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
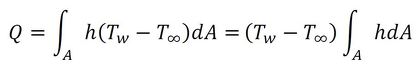 式12
式12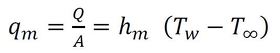 式13
式13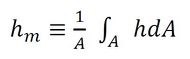 式14
式14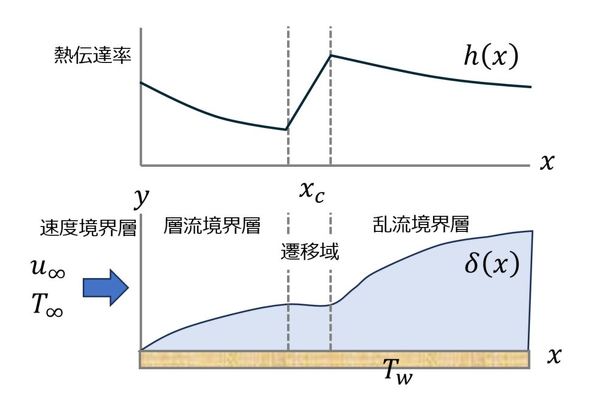
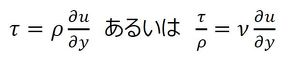 式15
式15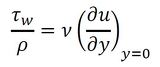 式16
式16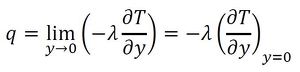 式17
式17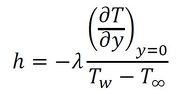 式18
式18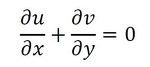 式19 連続の式
式19 連続の式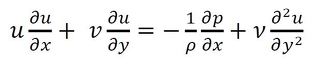 式20 運動方程式
式20 運動方程式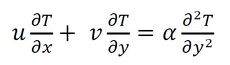 式21 エネルギー方程式
式21 エネルギー方程式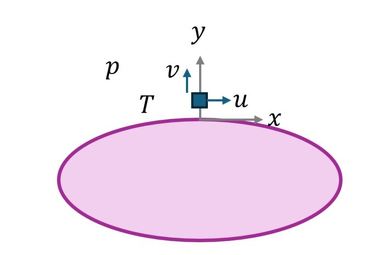
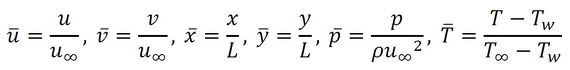 式22
式22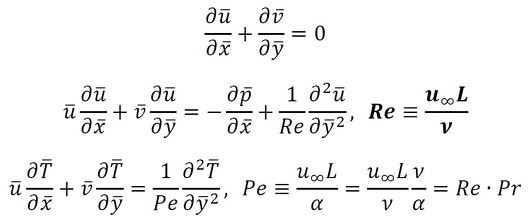 式23
式23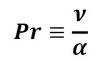 式24
式24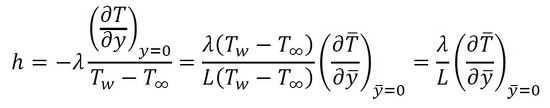 式25
式25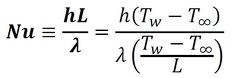 式26
式26





