CAEソフトに仕掛けられた2つ目のトラップ「応力特異点」を解決する:CAEを正しく使い疲労強度計算と有機的につなげる(6)(1/3 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第6回は、CAEソフトに仕掛けられた2つ目のトラップである「応力特異点」を取り上げる。
前回はCAEソフトに仕掛けられた1つ目のトラップである「1次要素の解析精度の悪さ」について述べました。今回は2つ目のトラップである「応力特異点」を解決します。
応力集中部の応力
前回取り上げた角Rのある事例(段付き板の曲げ問題)を再掲します。
応力集中係数αは図2でした。角Rがゼロに近づくと、αが無限大に近づきます。
さらに前回、下記の条件が成立している要素を使った場合に、要素分割を無限に細かくすると、有限要素法による計算結果は弾性力学による厳密解に近づくことも述べました。
- 節点変位が剛体変位の条件を満足するような場合に、要素内部でひずみを生じないこと
- 節点変位が一定ひずみ状態に与えるようなものであれば、変位関数は要素内において一定ひずみ状態を与えるものであること
- 変位関数によって計算されるひずみは、要素と要素の間の境界面上で有限であること
角Rがゼロの解析モデルで要素分割をどんどん細かくするとどうなるかというと、角Rがゼロの点の計算値が無限大に近づくことになります。このような点のことを応力特異点といいます。
応力特異点となる理由
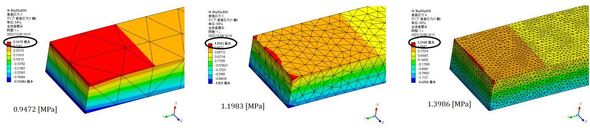
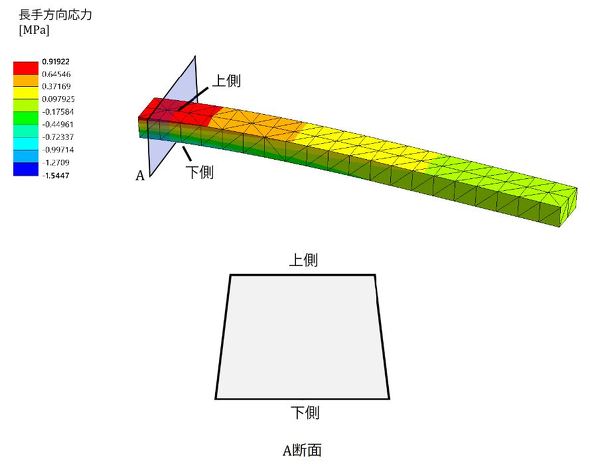
連載第1回で片持ちはりの応力を計算しました。図3に要素分割を細かくしていったときの長手方向応力を示します。
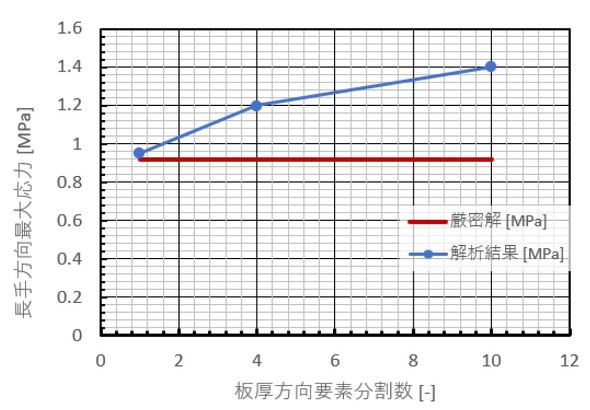
図4に板厚方向分割数と最大応力の関係を示します。板厚方向分割数を上げると最大応力(はりの根本の応力)が上昇しました。板厚方向分割数が1のとき、厳密解と一致していますが、これはたまたま一致したものだとお考えください。
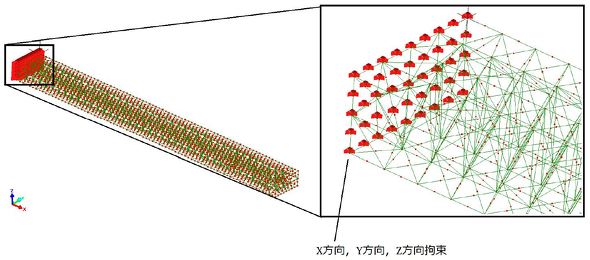
図5に、この解析の境界条件を示します。分かりやすいように、フリーの有限要素法ソフト「LISA」の画面を使いました。固定面の全ての節点のX方向変位、Y方向変位、Z方向変位を拘束しています。
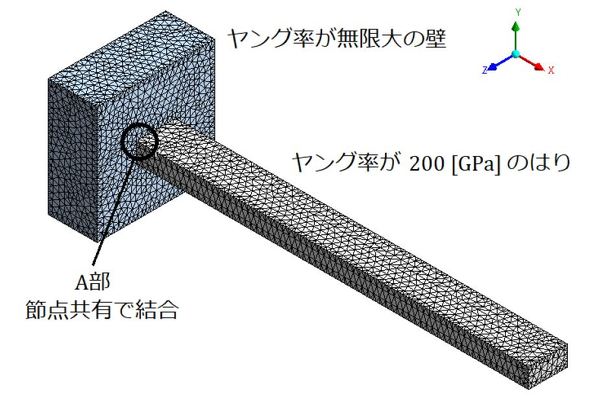
図5の境界条件を解釈すると、図6のようになります。はりと、ヤング率が無限大の剛体とが節点共有で結合された状態だと解釈できます。A部の角Rはゼロなので、応力集中係数が無限大となります。この結果、要素分割を細かくすればするほど応力値は大きくなると説明できます。
もう一つ、応力値がおかしくなった原因が考えられます。図7に、はりの変形を示します。はりの上面には引張応力が作用して伸びているので、体積一定だとすると幅方向に縮みます。はりの下面には圧縮応力が作用しているので、体積一定だとすると幅方向に膨らみます。ポアソン比が0.5[-]ではないので厳密には体積一定ではないのですが、幅の変化はあるはずです。
以上のことから、はりの断面は図7に示すように台形に変形しますが、図6のように、はりの根本はヤング率が無限大の壁に結合されているので、前述した台形への変形が阻害されてしまいます。この結果、はりの根元には幅方向成分の応力が発生します。また、この応力も根元で応力集中状態となります。そして、図7の断面内において上下方向にも伸び縮みがあり、同様に応力集中状態となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

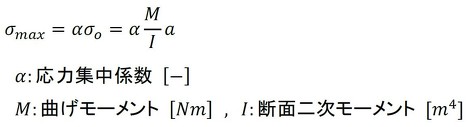 式1
式1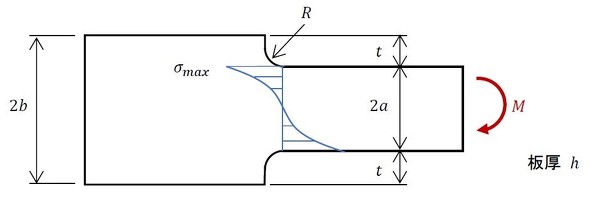
![応力集中係数 段付き板の曲げ(参考文献[1])](https://image.itmedia.co.jp/mn/articles/2406/11/ay4328_caefatigue06_fig02_w590.jpg)