CAEソフトに仕掛けられた2つ目のトラップ「応力特異点」を解決する:CAEを正しく使い疲労強度計算と有機的につなげる(6)(2/3 ページ)
CAE解析結果を厳密解と一致させよう
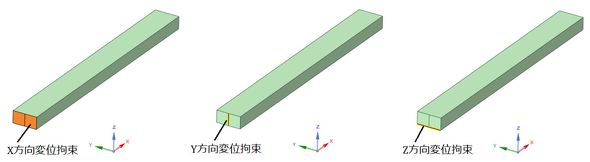
前述した理由を除外すれば、CAE解析結果と厳密解は一致するはずです。図7のような変形を許すような境界条件とします。図8に片持ちはりの境界条件を示します。図8左のX方向変位拘束は絶対必要ですね。図8中央のY方向変位拘束は、台形となるような変形を許しながら、剛体変位を阻止します。図8右のZ方向変位拘束は図7の断面内の上下方向の変位を許しながら、はりが重力方向に落下することを阻止します。
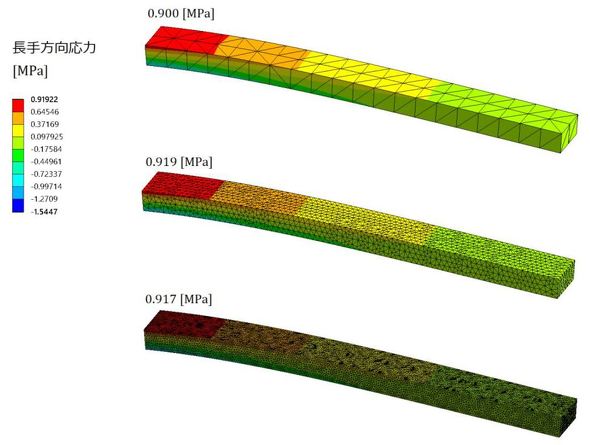
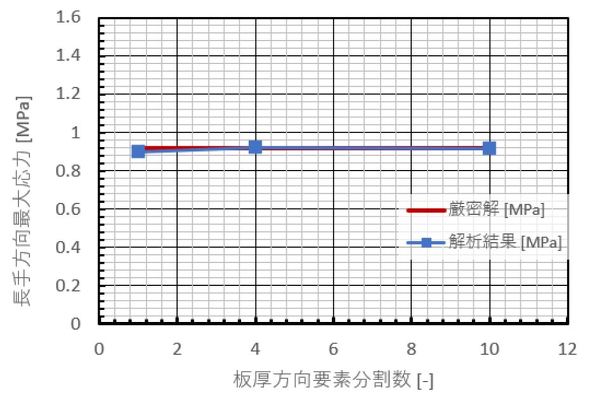
図9に解析結果、図10に板厚方向分割数と最大応力の関係を示します。解析結果は厳密解と一致しました。
板厚方向分割数が1の場合に注目します。分割数1でも厳密解と一致します。これは、「2次要素は要素内の変位が座標の2次式に従って変化し、応力分布は座標の1次式で変化する」との仮定に起因しています。はりの曲げの場合、長手方向応力は板厚方向に1次式で変化するので、上記の仮定に当てはまり、分割数1でもはり理論の厳密解と一致することになります。「有限要素法の出力はそもそも近似解で、要素分割を細かくしないと正確な値にならない」との先入観がぶっ飛びましたね。機械の部品には曲げ応力が発生している部分が多くあると思いますが、明らかに曲げだと思われるところは、板厚方向1分割でよいことになります。
連載第1回でシミュレーションの神様に見捨てられそうになりましたが、そう簡単に見捨てはしません(いやいや、筆者は最近でもCAEソフトが出力する理不尽なエラーメッセージに悩まされています……)。
N/mm2は使いたくない
ボルトシリーズでも解説したのですが、ちょうどLISAを使ったので、ヤング率と応力の単位について説明します。[N/mm2]の単位系で材料力学の講義を受けられた方もいると思いますが、筆者はヤング率と応力の単位に[N/mm2]を使うことに反対です。
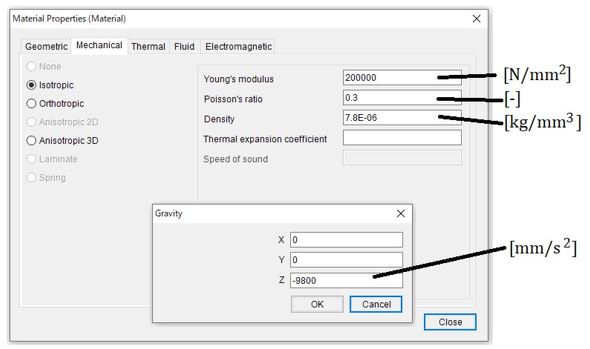
では、LISAで計算してみましょう。図11に材料定数の入力画面を示します。形状モデリングは[mm]で行いました。ヤング率は200000[N/mm2]となります(ゼロは5つです)。そして、密度は7.8×10-6[kg/mm3]です。
先に変位を計算しておきましょう。次式です(式2、式3)。
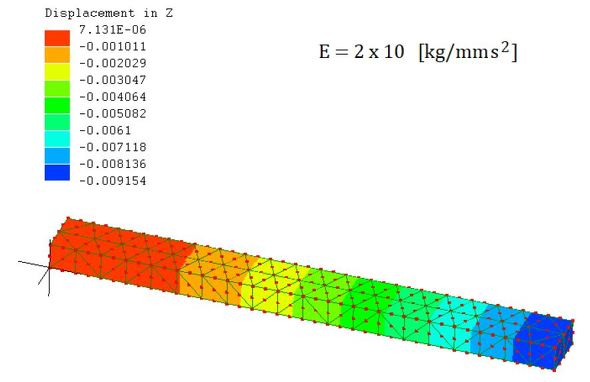
では計算しましょう。結果を図12に示します。
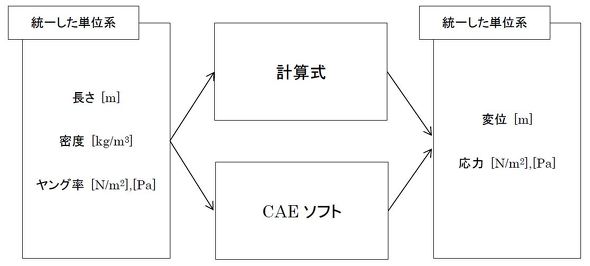
変位が9.18×10-3[mm]のはずが、9.15[mm]となりました。長さ200[mm]の鉄鋼材料が自重で9[mm]もたわむとは考えられません。どこかが間違っています。図13に計算式とCAE解析ソフトのお約束を示します。統一した単位系の数値を代入すると、統一した単位系の結果が得られます。
今回の場合はどうでしょうか。力の単位[N]を分解します。f=mαだったので、力の単位[N]は式4となります。
では、ヤング率の単位[N/mm2]はというと、式5となります。
式5を見ると、分子に[m]があって、分母に[mm2]があります。これは図13のお約束に反しています。「よくこんな単位で表記するよな」って感じで憤慨しております。では、mm-kg-s単位系でヤング率の単位はというと、式6となります。
このことはLISAのマニュアルにも書いてあります。では、前述したヤング率を設定して解析しましょう。結果は図14となり、たわみはほぼ式5の値となりました。
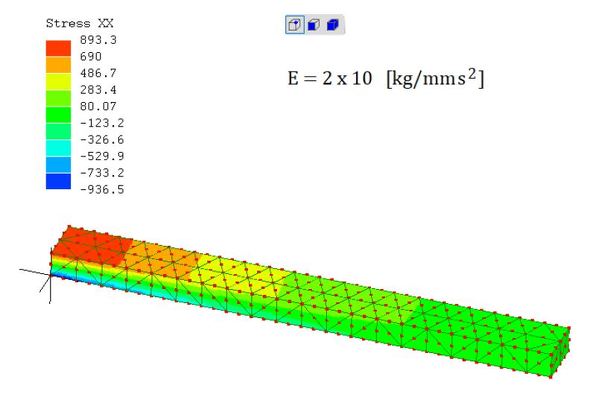
では応力はというと、図15になります。
応力値の解釈が必要になりました。応力とヤング率は同じ単位なので式6を使い、式7となります。
LISAでやっても板厚方向要素分割数が1で、厳密解と2.6[%]の差となりました。以上のことから、[mm]でのモデリング、200000[N/mm2]の単位のヤング率、7.8×10-6[kg/mm3]の単位の密度の組み合わせは使えません。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

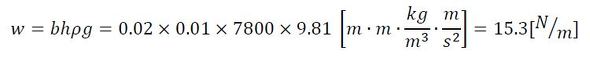 式2
式2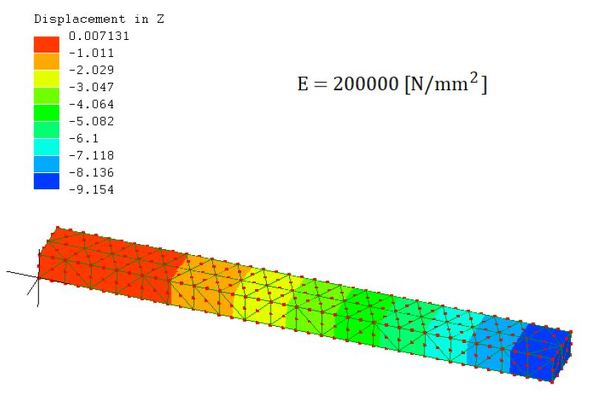
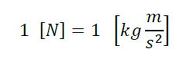 式4
式4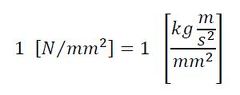 式5
式5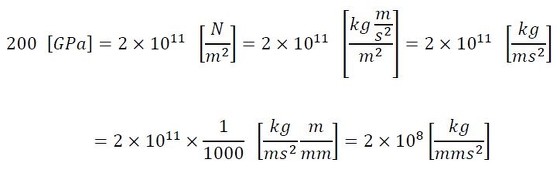 式6
式6