フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜:1Dモデリングの勘所(30)(3/5 ページ)
» 2024年04月17日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
ポンプ配管系への適用:解析例
以上から、解くべき式は2台ポンプ運転時の場合、下記となる。
上記の式および種々のパラメータを「Modelica」でテキスト表現すると以下となる(リスト1)。下記では、n1=n2=1500rpm、R1e=R2e=7×104kg/m7としている。この条件で流量、揚程はほぼ定格値となる。
model nuclearPump import Modelica.Constants.g_n; Real q; Real q1; Real q2; Real p1; Real p2; Real R1; Real R2; Real H1; Real H2; Real gam; Real N1; Real N2; Real Q1; Real Q2; parameter Real n1=1500; parameter Real n2=1500; parameter Real R=510; parameter Real R1f=520; parameter Real R2f=520; parameter Real R1e=7e4; parameter Real R2e=7e4; parameter Real L=2.55e4; parameter Real L1=1.82e4; parameter Real L2=1.82e4; parameter Real ro=1000; parameter Real Hrated=30; parameter Real nrated=1500; parameter Real qrated=2; parameter Real A=1.32; parameter Real B=-0.88; parameter Real C=1.45; parameter Real D=-0.89; equation q=q1+q2; p1=R1*q1*abs(q1)+L1*der(q1)+R*q*abs(q)+L*der(q); p2=R2*q2*abs(q2)+L2*der(q2)+R*q*abs(q)+L*der(q); R1=R1f+R1e; R2=R2f+R2e; p1=gam*H1; p2=gam*H2; gam=ro*g_n; H1=(A*N1^2+B*N1*Q1+C*Q1^2+D*Q1^3/N1)*Hrated; N1=n1/nrated; Q1=q1/qrated; H2=(A*N2^2+B*N2*Q2+C*Q2^2+D*Q2^3/N2)*Hrated; N2=n2/nrated; Q2=q2/qrated; end nuclearPump;
リスト1 Modelicaでテキスト表現した場合
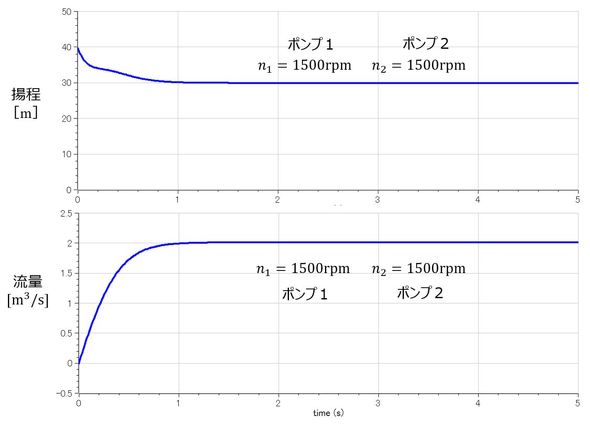
図4に、2台ポンプバランス運転時の解析例を示す。起動時には流体の慣性により、ポンプ揚程(圧力)は高くなるが、流れ始めると揚程も一定となることが分かる。2台とも同じ特性、同じ回転数なので、両者とも同じ挙動を示す。
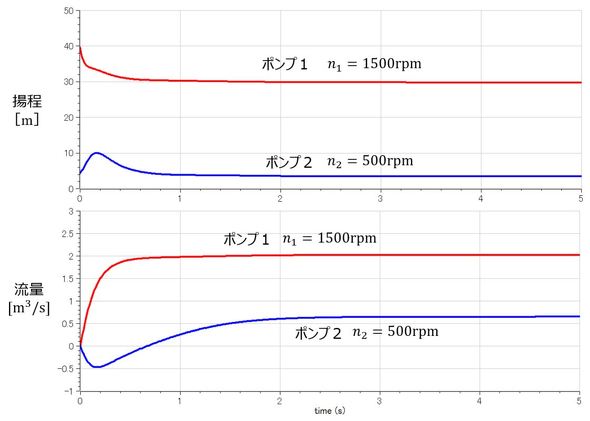
図5に、ポンプ1が1500rpm、ポンプ2が500rpmの2台ポンプアンバランス運転時の解析例を示す。ポンプ1の挙動はあまり変わらないが、低回転数側のポンプ2は最初、ポンプ1からの流れにより逆流が発生していることが分かる。このため、揚程も最初上昇している。
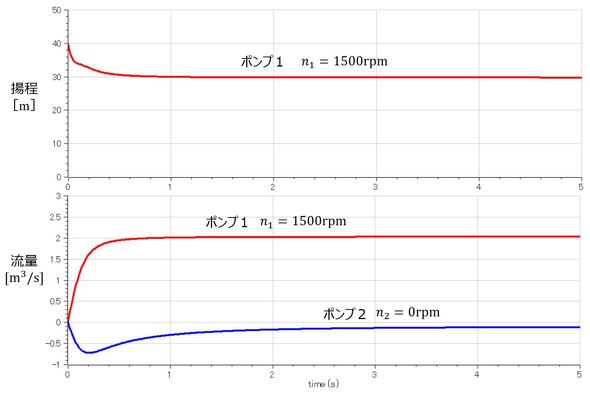
図6に、ポンプ2が停止したときの解析例を示す。停止ポンプにはポンプ1から常に逆流が発生していることが分かる。なお、図4〜6で条件が変わっても、ポンプ1の特性が見た目あまり変化していないのは、流量調整弁を各ポンプのすぐ下流に設置したことで、他ポンプの条件変化の影響を受けにくくなっているためだ。主配管にまとめて流量調整弁を設置すると、各条件でのポンプ1の特性は大きく変化する。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
Special SitePR
あなたにおすすめの記事PR
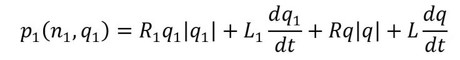 式14
式14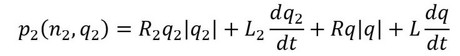 式15
式15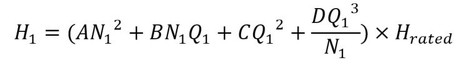 式18
式18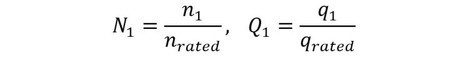 式19
式19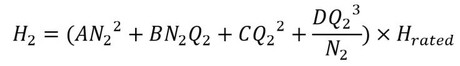 式20
式20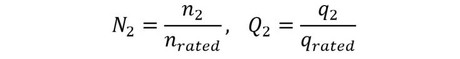 式21
式21