風車をモデリングする 〜風を電気エネルギーに変換する原理を起点に〜:1Dモデリングの勘所(24)(2/5 ページ)
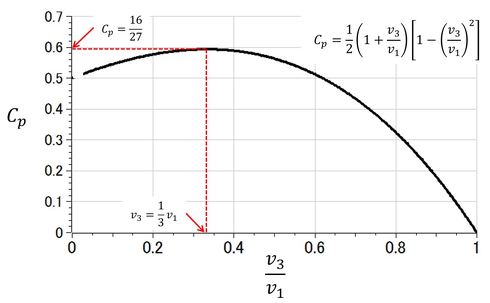
図4に示すように、
のとき、パワー係数は最大で
となる。一方、周速比(翼先端速度と風速の比)をλ=ωr/vとすると(rは翼径)、翼の回転数はω=vλ/rであるから、風が翼から受けるトルクは、
となる。
以上が風車のデザインを行う際の最も重要な原理である。すなわち、入ってくる風の速度vに対して、翼から出ていく風の速度がv/3となるように翼をデザインすればよい。具体的な方法は次節で述べるが、この際のデザイン因子は翼形状と翼枚数である。最近、よく見掛ける風車はほとんど翼枚数が3枚であるが、理論上は1枚でも、2枚でも、4枚以上でもよい。枚数が減ると風の抜けが良くなり過ぎる(出口風速が減速しない)ので、回転数(周速比)を増やして風をブロックする必要がある。
例えば、1枚翼の場合には3枚翼の2倍以上の周速比(回転数)が最適値となる。そうすると、遠心力が1桁大きくなり、強度上問題となる。一方、4枚以上の多翼では周速比(回転数)は低くできるが、回転体としてのバランシングや重量に加え、これらに伴う製作費、据え付け費の問題が出てくる。以上を勘案して3枚翼が多く取り入れられている。
今回は、発電用の風車を対象としているので、発生パワーの最大化が目標であるが、歴史的には風車は粉ひきなどの動力として使われてきた。この場合には、発生トルクの最大化が目標となり、周速比(回転数)の低い多翼風車が有利となる。風車の詳細に関しては参考文献[1]を参照されたい。
参考文献:
- [1]牛山泉|風力エネルギーの基礎|オーム社(2005)
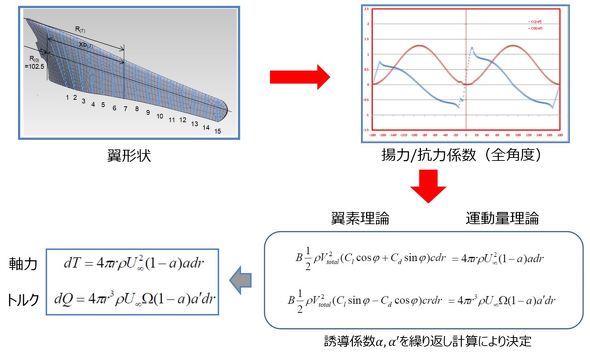
翼の発生トルクの算定手順
翼の発生トルクを見積もる手順を考える。図5にその手順を示す。
最初に翼形状を定義する。次に、翼形状(一般に長手方向に異なる)の各断面の揚力係数/抗力係数を定義する。風車翼の場合、全ての角度から風が入射するので全角度定義する必要がある。この際、各種データベースを用いてもよいし、実験的に求めたり、CFD(数値流体力学)解析を適用したりしてもよい。
ここまでが準備段階で、次に実際に翼が風を受けてトルクに変換するプロセス/現象を理解し、定式化する。具体的には、翼素理論と運動量理論を組み合わせて、誘導係数という概念を導入し、繰り返し計算により誘導係数を算出して、トルクを求める(詳しくは、参考文献[2]を参照)。さらに、求めたトルクはある翼断面でのトルクであるため、これを長手方向に積分して、翼枚数を考慮した全トルクを算出する。トルクだけでなく抗力(軸力)も併せて計算する。軸力は翼が風から受ける力で塔の強度設計に必要となる。
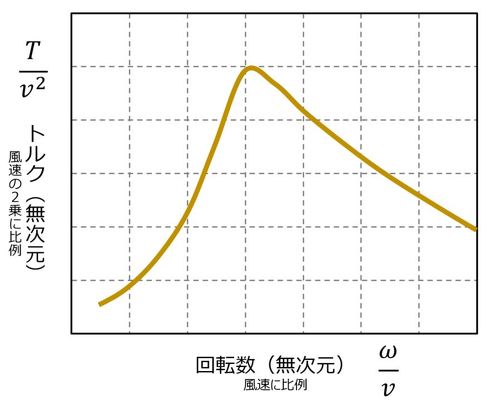
図5の手順で算定した翼の性能(トルクと回転数の関係)を図6に示す。
実際には、翼形状と翼枚数を決めて(市販の小型風車の翼を計測、入力データとした)、図5の手順でさまざまな風速、回転数でトルクを算出し、この結果を無次元化してグラフ表現したものが図6である。なお、図5の計算は「Excel」で行っている。この縦軸と横軸を乗じた値がパワーである。このように一見複雑な特性となるが、最適なパワーを有する条件が存在するとともに、基本的には回転数は風速に比例し、トルクは風速の2乗に比例する。すなわち、パワーは風速の3乗に比例する。
参考文献:
- [2]Wind Energy Explained, Theory, Design and Application, Second Edition|John Wiley & Sons Ltd.(2009)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
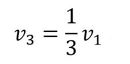 式10
式10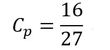 式11
式11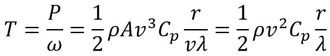 式12
式12