振動シミュレーションを理解する 〜CAEソフトによるモーダル解析〜:CAEと計測技術を使った振動・騒音対策(11)(2/3 ページ)
CAEソフトによるモーダル解析(続き)
次に表2の解説Bです。連載第8回のばね−マス系では“振幅を小さくしたいなら、ばね定数を大きくすべきだ”と述べました。これは、共振などを無視したかなり乱暴な主張でしたが、剛性を高くすると多くの振動問題は解決の方向に向かいます。ばね定数を大きくすると共振周波数も高くなるので、振動を小さくしたい場合は、モーダル解析結果の振動形状を見て、変形している根元の形状を変えることになります。
連載第8回の式27を参考にして、断面二次モーメントを大きくする方向に形状を変えたり、長さを短くしたりして、モーダル解析をやり直し、固有振動数がどうなったかで設計案の良否を判断します。モーダル解析結果の変位や応力は正規化されたもので、その大きさには意味がありませんが、応力分布をアニメーション表示すると設計変更すべき場所が一目瞭然となります。ちなみに、CAEソフトの設定がデフォルトのままだと応力表示ができない場合がありますので、その場合は設定を変更してモーダル解析結果の応力を表示できるようにしてください。応力を表示した例を動画4に示します。
動画5は「モード7」の相当応力分布です。応力の大きさから板が怪しいことが分かります。しかし、たくさんある振動モードの中からなぜモード7を選んだのかは、後に説明する時刻歴応答解析や実験モーダル解析をしなければ分かりません。
表2の解説Cでは「モーダルパラメーター」が分かります。モーダルパラメーターとは、それぞれの振動モードの等価的な質量、ばね定数、減衰比などです。「何これ、どうするの?」となりますが、後に行う時刻歴応答解析や周波数応答解析に必須の情報となります。
モーダル解析結果の振動形状が意味するもの
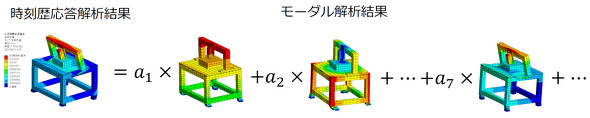
モーダル解析結果の振動形状はたくさん出てきますが、これらは将来共振状態になる可能性のある振動形状です。機械の振動問題で困っていたならば、このときの振動形状はモーダル解析結果の振動形状のどれか1つか複数の和と考えることができます。モーダル解析結果の筆者なりの解釈を述べたいと思います。
筆者は「たとえ話は理解をさらに妨げる」と思っていますが、それを承知で「フーリエ級数」をたとえ話のネタとします。フーリエ級数の式を式1に示します。連載第4回の式7は間違っていましたね。次式に差し替えてください。
フーリエ級数を使うといろいろな関数をsinとcosの和で表すことができます。sinとcosの和の数を増やせば増やすほど元の関数に近づきます。矩形波をsinの和で表した例を図1に示します。図1左図に示したようにnを増やしていくとsinとcosの和は黒線の矩形波に近づいていきます。図1右図のようにn=27までやるとかなり近づきました。
モーダル解析結果もフーリエ級数と同様に考えることができます。実際の振動は、それぞれのモーダル解析結果に係数を掛けた和として表すことができます。振動を起させる外力が変わると係数が変わると考えてよいかと思います。無理やり式で書くと式2となるでしょうか。
係数anは、ほとんどのモードでゼロに近い値になります。
式2を図示すると図2になります。この場合はa1とa7がある値を持っていて、それ以外の係数はゼロに近いようです。フーリエ級数の場合は黒線のように角がとがっているので、nを大きくとらないと元の関数になかなか近づかないのですが、振動変位は角がとがっているような波形ではないので、式2の場合は数個の振動モードで十分なことが多いようです。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


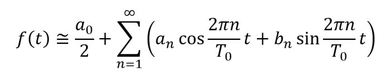 式1
式1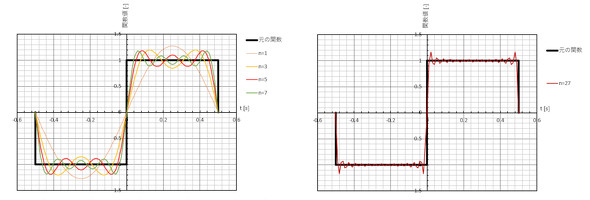
 式2
式2