振動低減の戦略 〜ばね−マス系の振動【2】〜:CAEと計測技術を使った振動・騒音対策(9)(4/5 ページ)
伝達関数をグラフで表現する
式8と式15が同じ形なので、質点に力が作用したときの床に伝わる力と、床の振動変位による質点変位については一緒に説明します。伝達関数なのですが、前者を「力の伝達率」、後者を「変位の伝達率」と呼びましょう。
前回と同様にs=jωとし、減衰比ζ、無減衰固有角振動数ωno、無減衰固有振動数fnoを導入すると、振動伝達率τは次式値なります。
横軸を周波数ではなく、周波数を無減衰固有振動数fnoで割った値として、伝達率をグラフ化したものを図3に示します。周波数がfnoと一致したとき、つまりf/fno=1[-]のときにほぼ共振状態となります。f/fno=0[-]のときを考えます。図3は対数グラフなのでf/fno=0.1[-]の値を延長してください。伝達率は1[-]となります。例えば、図1において質点に作用する力が変化せず上方向に引っ張り続けている場合となるのですが、ダッシュポットは伸び切っており、ばねを介して質点に作用している力がそのまま床に作用することになり、力の伝達率は1[-]です。図2においては、床が変位してそのままずっと変位し続けていたら、質点は床の変位量と同じとなり、変位の伝達率は1[-]となります。伝達率が1[-]というのはこのような意味です。
伝達率を実際の機械に当てはめる
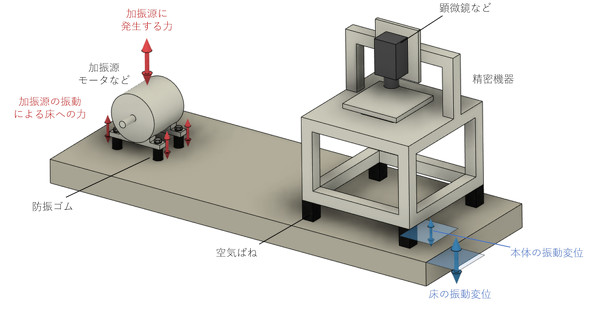
図4に振動絶縁の例を示します。図4左側はモーターが防振ゴムを介して床に固定されている例で、モーターの回転バランスが取れていないとモーターの回転数と同じ周波数の加振力が発生します。モーターの質量をm、防振ゴムのばね定数を4kとして伝達率を計算することになります。防振ゴムは4個使いなので、ばねは並列つなぎとなり、ばね定数は防振ゴム1個のばね定数の4倍です。図4右側は装置の質量をm、空気ばねのばね定数を4kとして伝達率を計算します。実は、ばね定数を4kとするのは少し危険側の見積もりで、モーターが回転振動するときはばね定数を2kとし、モーターの回転に対する運動方程式を立てなければなりません。「モーターの回転」と書きましたが、モーター軸の回転ではなく対角にある2つの防振ゴムを通る線を軸とし、モーター全体が剛体として回転しているイメージです。
ζがどのような値になるのかを調べる必要がありますが、あまり性能の良くない防振ゴムだと仮定してζ=0.50[-]とし、伝達率を0.1[-]以下とするのであれば、動画3からf/fnoは10[-]以上とする必要があります。mは分かっているので、式19から適切な防振ゴムのばね定数を求めることができます。ネット検索するとたくさんの防振グッズが出てきますが、適切なばね定数の防振ゴムを選択する必要があるため、本当に必要となるものはネット上のごく一部となります。
床からやってくる振動を絶縁するのはかなり難しいです。ネット検索で見つかる防振ゴムはほぼ使えないでしょう。建物の2階以上の床の上下方向の振動数は11[Hz]くらいです。かなり小さなばね定数の防振ゴムが必要となり、ゴム材料では満足できるものはなく、空気ばねを選択することになります。つまり、風船の上に装置を置くことになります。目標とする伝達率を0.1[-]、空気ばねのζを0.05[-]とすると、必要とする固有振動数比は次式となります。
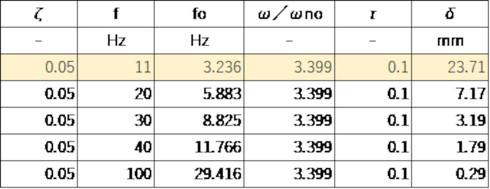
機械の質量は簡単に分かるので、式18から必要とするばね定数が求まります。ここでは、ばねの上に装置を載せたとき、装置の自重によってばねがどの程度沈み込むかを求めてみます。式18を用いると、沈み込み量δは次式となります。
式21にいくつかの数値を代入しました。表1となります。11[Hz]の床振動を絶縁できる状態を作ったのならば、そのとき装置は自重によって23.7[mm]沈み込んでいます。とても柔らかいばねが必要だということをご理解いただけると思います。「パッシブ除振ユニット」でネット検索すると、これに適した空気ばねを見つけることができます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

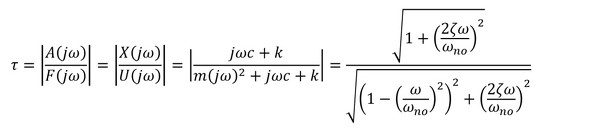 式16
式16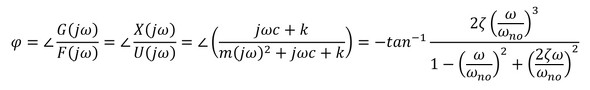 式17
式17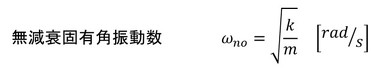 式18
式18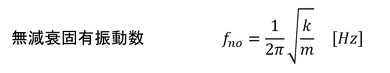 式19
式19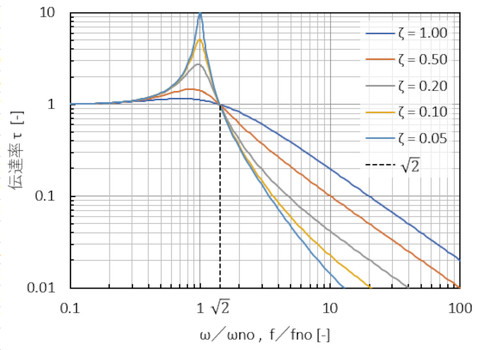
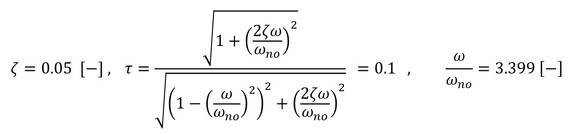 式20
式20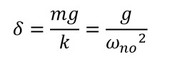 式21
式21