非線形の問題は一体どのように解くの? 解析ソフトはどんな計算をしているの?:いまさら聞けない 非線形構造解析入門(6)(1/2 ページ)
多くの3D CADではオプションとしてCAE機能が用意されているが、ほとんどの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。最終回となる連載第6回では、Newton-Raphson法(ニュートン法)を取り上げつつ、非線形解析ソフトがどのように解析の計算を進めているのかについて解説する。
非線形の問題は、線形の問題のように単純な四則演算では解けません。この件については、ごく簡単に連載第1回で触れています。では、どのように解くのか? といえば、増分解法によって少しずつ最終的に求めたい解に近づくように結果を求めていきます。その手法の代表格で、多くの商用解析ソフトで採用されているのが「Newton-Raphson法(ニュートン法)」です。
今回は、Newton-Raphson法を取り上げつつ、非線形の解析ソフトがどのように解析の計算を進めているのかについて解説します。
非線形解析ソフトでよく用いられているニュートン法
簡単に連載第1回を振り返っておくと、線形の問題というのは、言ってみれば「1次方程式を解く」ということになります。従って、
という式があって、aが定数、与えられたyについて、未知数xを解くのであれば、これは単純にx=a/xというシンプルな割り算で解を求められます。このように、線形の問題であれば四則演算で解を求めることができるのですが、式2のような2次方程式の場合はちょっと様子が変わってきます。
式2で与えられたyについて、xを解くのであればx=√y/aとなり、単純な四則演算では解が求められません。ちなみに、有限要素法で解を求めるということは、つまり連立1次方程式を解くということになります。この点についても、これまでの連載の中で説明しています。
では、どうするのか? というと、最終的に求める解に到達するために、一度に問題を解くのではなくて、増分解法を用いて、誤差を取り除きながら少しずつ答えを求めていきます。そのような増分解法の1つが、Newton-Raphson法と呼ばれる手法で、非線形解析ソフトのプログラムでよく用いられています。ごく簡単に言えば、現在分かっている所から始めて、段階的に計算を進めていき、最終的に目的の結果を求めるというアプローチです。
増分解法の基本的な考え方/Newton-Raphson法のイメージ
ということで、ここで増分解法の基本的な考え方を説明します。
Newton-Raphson法とは、非線形方程式を数値的に求める方法の1つです。その式が微分可能な方程式であるとき、微分をしなくても解が求まります。また、繰り返し計算を行うことで、本来の解に近づけていくことができます。
参考までに、Newton-Raphson法による√3の求め方を示します。
Newton-Raphson法では、f(x)=0で示される式の解を反復計算によって求めるわけですが、各反復ステップは式3で定義されます。
ここでのnは、0、1、2、3……となります。
まず、√3というのは、x2−3=0で表せる式で求まる解の1つです。そこで、関数f(x)を考えたとき、f(x)=x2−3となります。
図2は、これをグラフで示したものです。
ここで方程式f(x)=0を、Newton-Raphson法で反復計算していきます。
さて、ここから繰り返し計算を始めますが、初期値が重要となります。中学校の数学から私たちは、答えが約1.732であることを知っていますが、ここでは初期値を4としてみます(x0=4)。
f(x)の微分は式4の通りです。
従って、最初の反復ステップは式5のようになります。
1回の反復では、とても近いとはいえない値ですので、反復計算を続けます。2回目の反復は式6の通りです。
結果としてはだいぶ近くなってきましたが、もう一息といった感じなので3回目の反復をしてみます(式7)。
3回目の反復で、一般的に使用される1.73まで数値が合ってきました。つまり、実用上はこの程度の反復でも十分に使えると考えてもよいでしょう。以上、Newton-Raphson法のイメージを簡単に紹介しました。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞


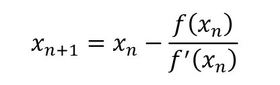 式3
式3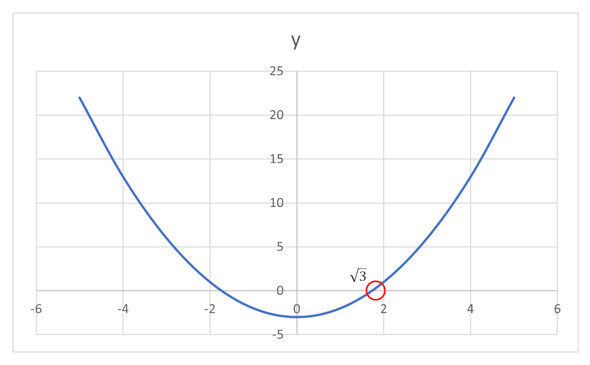
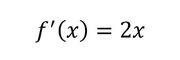 式4
式4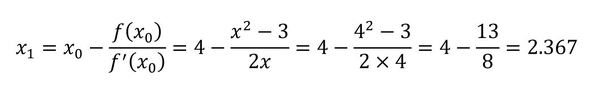 式5
式5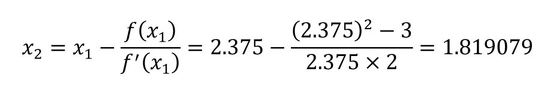 式6
式6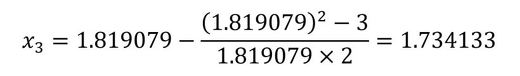 式7
式7





