領域最適化のアルゴリズムについて考える:フリーFEMソフトとExcelマクロで形状最適化(12)(2/6 ページ)
領域最適化のアルゴリズム(続き)
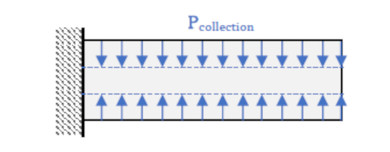
最適化後の領域の体積の目標値Vtargetも設定しましょう。2次元問題なので体積は(面積×板厚)となります。体積が目標値よりも大きくなったら全体の体積を縮小させるような荷重をかけます。図4のような荷重です。
Pcollectionは次式で決定します。
Rcollectionは人間が決める定数です。無次元数で1桁か2桁の数です。|Popti|aveは式2のPoptiのベクトルの大きさの平均値です。Pcollectionの大きさのオーダーをPoptiの大きさのオーダーに合わせるために導入しました。Vtarget、Vcurrent、Vinitialは以下の通りです。
- Vtarget:体積の目標値
(Vinitial:×1)となるようにExcelのセルに計算式を入れておく - Vcurrent:現在の解析対象の面積
- Vinitial:第1世代の解析対象の面積
式4の分子に(Vtarget−Vcurrent)があります。これは(目標値−現在値)に比例する量を対象物に与えるという意味で、フィードバック系が作られていることになり、「P制御(Proportional Controller)」となります。参考文献[1]では「PID制御(Proportional Integral Differential Controller)」を採用しています。こちらの方がデラックス感があるのですが、以下のような理由から、P制御で十分だと考えています。
通常のコンピュータを使った制御では1秒間に数千回以上、アナログ回路で制御系を構築したら無限回だけ制御ループを回すのに対し、領域最適化では十数回の繰り返しで最適化が完了します。I制御では積分をするのですが、十数回の繰り返しでは、被積分データをそろえることができず、I制御が成立しません。D制御では微分をして、現在値を目標値に早く近づける作用があるのですが、D制御のゲインを大きく取ると、図5のようなオーバーシュートや振動が生じます。これらを避けながら、早く目標値に近づけられるようにD制御のゲインを決めるのには数十回の計算が必要です。
PID制御のそれぞれのゲイン3個は、制御ループをたくさん回して実験的に決めることになるのですが、たとえP制御のゲインが決まったとしても、I制御を追加したらP制御のゲインを少し下げなければなりませんし、D制御を追加したら、P制御のゲインとI制御のゲインをまた変更することになります。3つも未知数があっては、何回の実験が必要になるでしょうか。たかだか十数回の繰り返しをするだけなので、この投資は回収できません。よって、P制御だけで十分です。
次の世代の形状を決めるための荷重は、次式となります。
Poptiを表す式2の第2項とPcollectionが、式1のΛに相当すると解釈しています。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

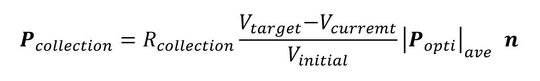 式4
式4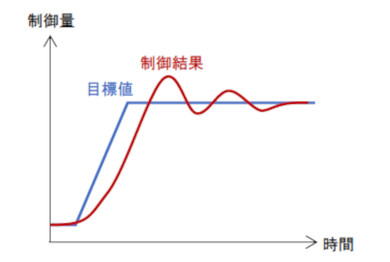
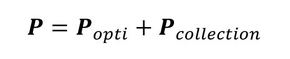 式5
式5





