領域最適化のアルゴリズムについて考える:フリーFEMソフトとExcelマクロで形状最適化(12)(5/6 ページ)
1次要素と2次要素
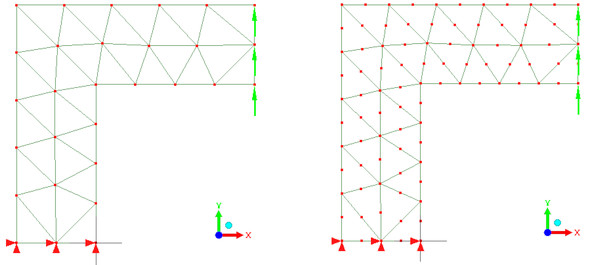
トポロジー最適化では、1次要素を使いました。3節点三角形要素、4節点四角形要素です。領域最適化では2次要素、6節点三角形要素、8節点四角形要素を使います。3節点三角形要素と6節点三角形要素を使って、1次要素と2次要素の違いを説明します。
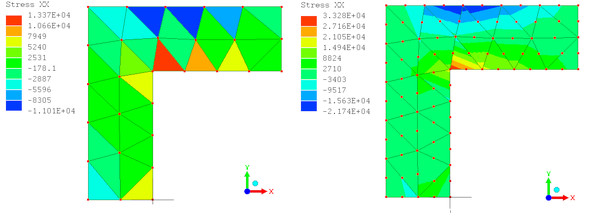
図9のような問題を解析してみます。X方向応力分布(要素解)を図10に示します。
1次の三角形要素では要素内の応力が一定値となります。それと比較して、2次の三角形要素では要素内で応力が変化しており、応力集中が発生していることが分かります。領域最適化では、高応力部の形状を変えて応力を平たん化することを目的としているので、2次要素は必須となります。
応力の計算結果がなぜこのように違うのかを少し解説します。1次要素(3節点三角形要素)では、要素内の変位(u,v)を座標の1次式で表せるとして剛性マトリクスが作られています。変位は次式となります。
ひずみは変位を座標で微分したものでした。次式で、ひずみは座標に関係なく一定値となります。
応力は次式で表されます。各ひずみ成分の線形結合なので、応力も座標に関係なく一定値となります。1次要素による応力分布が要素内で一定値であるということには、その解析精度の低さに少しショックを受けられた方もおられるかと思います。しかし、昔は「応力とひずみが要素内で一定値であっても、今まで手も足も出なかった弾性力学の方程式が解ける」ので、これで十分満足していたものでした。
2次要素(6節点三角形要素)では、要素内の変位(u,v)を座標の2次式で表せるとして剛性マトリクスが作られています。(u,v)の近似式を以下に記します。
ひずみは次式で、座標に対して1次式の形で変化します。
応力は、式15から各ひずみ成分の線形結合なので、座標に対して1次式の形で変化します。よって、応力集中部を見つけることができます。図10を見れば、大きな応力が発生している場所と小さな応力が発生している場所の領域の形状を変更して領域全体の応力を均一化するには、2次要素の結果を利用しなければならないことは分かると思います。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

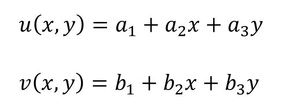 式13
式13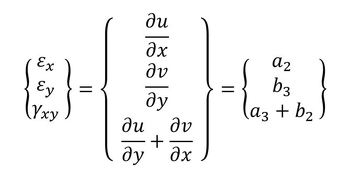 式14
式14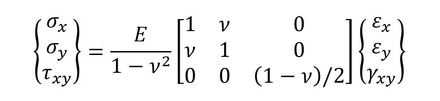 式15
式15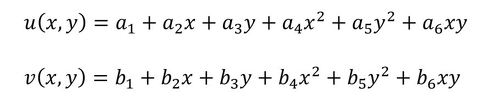 式16
式16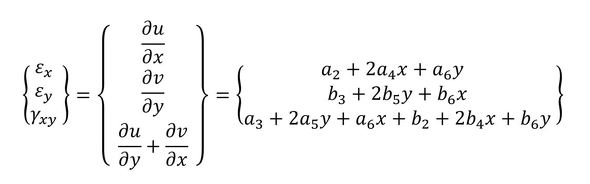 式17
式17





