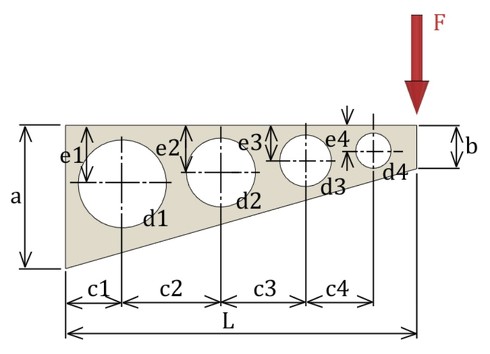
　例えば、図6のような部品の設計を考えてみましょう。形状が幾つかのパラメータで定義されています。荷重Fによる変形量を最小化ないしは、最大発生応力を抑え応力がどこでも同じになるような設計パラメータを求める問題となります。通常、初期パラメータを決めて3D CADに付属しているCAEソフトで解析し、パラメータを何通りか作って解析して、その中から最も良いものを選ぶ方法がとられると思います。筆者はこうしたアプローチを「パラメトリックスタディ」と呼んでいました。パラメータの設定に「タグチメソッド」を使うのもよいかと思います。

図6　パラメトリック設計［クリックで拡大］

　では、最終的に選んだパラメータは本当に最適なものでしょうか？　その保証はありません。例えば、「荷重Fによる変形量を最小、つまり剛性最大となる」パラメータが選ばれていることが数学的に保証されているでしょうか。次回お届けする連載第2回では、片持ちはりを例に「ラグランジュの未定乗数法」（参考文献［1］）を用いて、剛性最大となる片持ちはりの形状を求めます。

参考文献：

［1］ラグランジュの未定乗数法／Wikipedia

2．トポロジー最適化

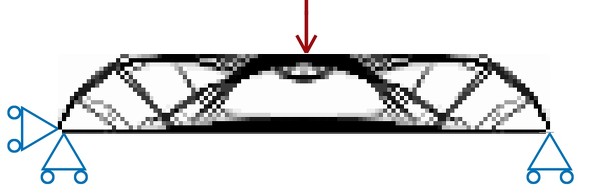
　トポロジー最適化の技術を使うと、図1に示したようなアーチ橋の形状をソフトウェアが考え出してくれます。生まれて一度もアーチ橋を見たことのない人が橋の設計をする際、この形状を思い付くまでにどれくらい時間がかかるでしょうか。設計者ならぜひ使ってみたい技術です。

　例えば、材料費低減のための肉抜きで、要求するような条件を満たしながら、どこにどのような形状の穴を開けるべきか教えてくれます。要求するような条件として、「剛性を最大化する」「最大発生応力を抑え、応力を均一化する」「荷重点ではない指定した位置の変位を最小化する」などがありますが、ここで取り上げるのは「剛性を最大化」しながら、指定した割合で体積を減少させた解を求めます。つまり、体積を元の40［％］に減らすのですが、べらぼうな位置で肉抜きするのではなく、剛性を最大限維持しながら肉抜きします。

　両端支持はりを肉抜きした例を図7に示します。両端支持はりの場合、中央で曲げモーメントが最大になるので中央部はあまり肉抜きしていませんが、支持点近傍は曲げモーメントがゼロに近づくのできゃしゃな構造で大胆に肉抜きしてあります。鋳物や射出成形品の設計に活用できそうです。そして、たいがいの場合、剛性最大化の解の応力分布は均一なものとなり、強度的にもムダのない形状になっています。

図7　両端支持はりを肉抜きした例［クリックで拡大］

　トポロジー最適化の技術は、参考文献［2］により1988年に発表されました。それから約30年たち、トポロジー最適化機能はハイエンドFEMソフトウェアと一部の3D CADに付属し普及してきました。ただし、高価です。そして、誰がやっても同じような答えを出すので、設計者のセンスを生かすことができません。

　本連載では、1300節点まで無料で使えるFEMソフト（LISA）とExcelを使ってトポロジー最適化を行うのですが、LISAの入力ファイル生成と解析結果読み取りの部分だけマクロプログラムとし、最適化のアルゴリズムはExcelのシートに計算式として組み込みます。シートを書き換えれば、オリジナルのアルゴリズムでトポロジー最適化を試せるようにするつもりです。数学的な厳密性はちょっと脇に置いて、剛性最大、体積最小のオリジナルな解を見つけてみるのもよいかと思います。

参考文献：

［2］Bendsøe, M. P. and Kikuchi, N.：Generating optimal topologies in structural design using a homogenization method／COMPUTER METHODS IN APPLIED MECHANICS AND ENGINEERING 71，p197-224（1988）

3．領域最適化

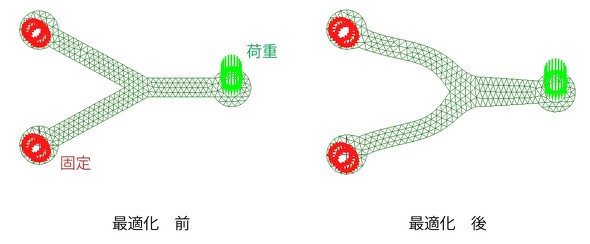
　3つ目は、領域最適化です。いわゆる“形状最適化”のことですが、形状最適化にはトポロジー最適化も含まれるので「領域最適化」という言葉を使いました。設計パラメータを求めているわけではないので「ノンパラメトリック最適化」とも呼ばれています。図8にリンクの形状を改善した例を示します。

図8　領域最適化例［クリックで拡大］

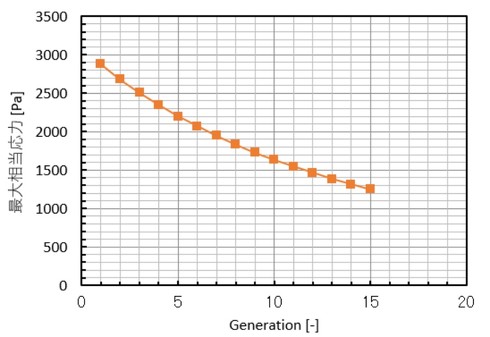
　相当応力の最大値の変化を図9に示します。相当応力が2900［MPa］から1300［MPa］に低減しました。初期値である2900［MPa］には、応力特異点による過度な応力集中を含んでいますが、これを差し引いても効果が確認できます。図を見るとまだまだ応力を低減できそうですが、あまり形を変えると他の部品と干渉してしまうのでこの辺にしておきました。この手法は、設計計算時に応力が許容応力を上回った場合に活用できると思います。トポロジー最適化ほどの派手さはないのですが、実用的な最適化手法です。