ボルト締結部の有限要素法モデルの比較と部分固着モデルの提案：設計者向けCAEを使ったボルト締結部の設計（8）（4/5 ページ）

[高橋良一／ＲＴデザインラボ 代表，MONOist]

4．リベット接触モデル

　これは、筆者が勝手に命名したモデルですが、特にテクニカルなことはなく、ボルト締結を忠実にモデリングしたものです。ボルトのねじ山はモデリングせず、リベットのような形になったので「リベット接触モデル」と呼ぶことにしました。

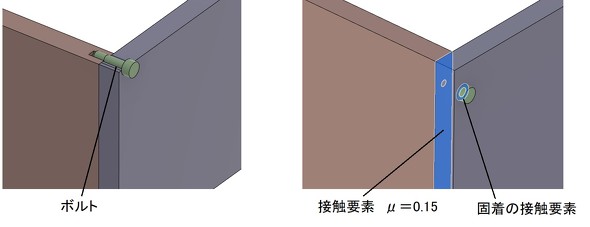
　解析モデルを図12に示します。図12左側の緑色の部品がボルトです。また、図12右側にある通り、板同士の接触面には摩擦係数0.15の接触要素を設置します。接触要素とは、部品同士が接触しているときは反発力が発生し、接触している部品同士が貫入することはありませんが、離れるような力が作用しているときは自由に離れます。そして、部品同士が滑ることができ、そのときの摩擦係数を設定することができます。ボルトの頭と板との接触面は離れることがないだろうと考え、固着の接触要素としました。固着モデルと同様です。

図12　リベット接触モデル［クリックで拡大］

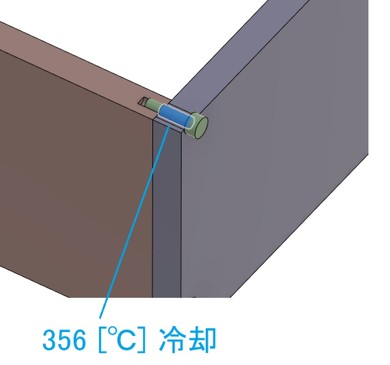
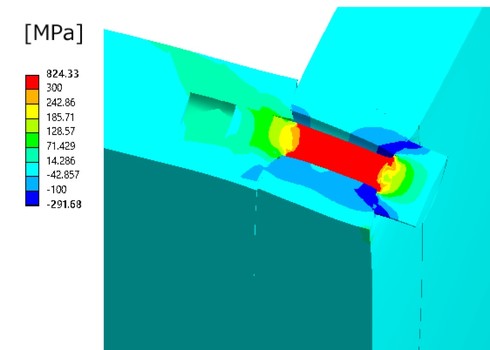
　次に、ボルトの初期締結力を再現します。今回は図13の青色で示す領域を356［℃］冷却収縮させて、2460［N］の初期締結力を発生させました。そのときのボルト軸方向応力分布を図14に示します。

図13　ボルト初期締結力の発生［クリックで拡大］

図14　ボルト軸方向応力分布［クリックで拡大］

　今までの解析は、全て線形解析でモーダル解析が可能でしたが、今回は接触要素を使っているため、非線形解析となりモーダル解析を実行できません。そのため、時刻歴応答解析で固有振動数を求めました。

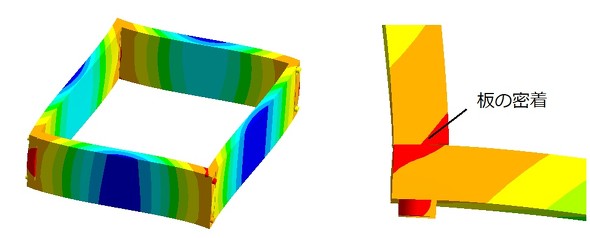
　荷重ステップ1で熱収縮させ、荷重ステップ2で板の稜線にステップ状の強制変位を与え、構造体が時々刻々と変形する様子を求めました。図15に構造体の変形図を示します。ボルトの締結力によって、板同士が密着しています。

図15　リベット接触モデル変形図［クリックで拡大］

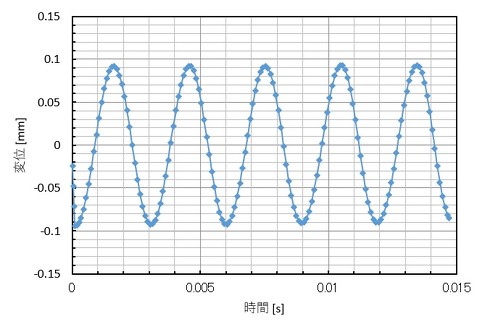
　図16に時刻例応答解析で求めた、ある節点の変位を示します。この図からでも固有振動数は求まりますが、念のため離散フーリエ変換して振動数を求めたところ、341.8［Hz］となりました。実測値にかなり近づくことができました。

図16　時刻歴応答解析の結果（ある節点の変位）［クリックで拡大］

4種類の有限要素法モデルを比較した結果

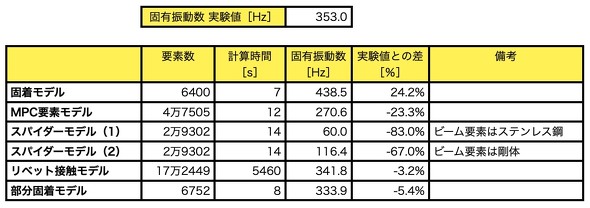
　ここまで、4種類のボルト締結部の有限要素法モデルを説明しました。結果を表1にまとめます。

表1　ボルト締結部の有限要素法モデルの比較［クリックで拡大］

　固着モデルは、要素数が6400［個］と断然少なく、計算時間も7秒と使いやすいのですが、「危険側の見積もり」をしてしまうので注意が必要です。

　MPC要素モデルは、ボルトの穴をモデリングしたため要素数が増えましたが、最近のPCは性能が良いので計算時間は12秒です。そして、固有振動数が低めに算出され、これは「安全側の見積もり」になります。有限要素法ソフトによっては、MPC要素の設定は結合したい面をクリックするだけでできるのでオススメです。

　スパイダーモデルは、残念な結果となりました。ビーム要素のヤング率を調整しても固有振動数は実験値に近づきませんでした。前述したように、ボルトのレイアウトを2列2本にしたり（4本止め）、ソリッド要素ではなくシェル要素を使ったりするともっと良い結果となりますので、がっかりしないでください。

　リベット接触モデルは、ほぼ実験値と同じ値になりました。この結果を出すためにいろいろな合わせ込みはしていません。1発でできました。しかし、要素数が増えたこと、そして、接触要素を使ったためにモーダル解析ではなく時刻歴応答解析になったことから、5460［s］の計算時間となりました。これでは、部品点数が数十あるアセンブリモデルへの適用は、手間と要素数と計算時間の観点から現実的ではないように思えます。何か良いアイデアはないでしょうか。