金属材料の摩擦係数:設計者向けCAEを使ったボルト締結部の設計(5)(2/3 ページ)
摩擦係数の決定
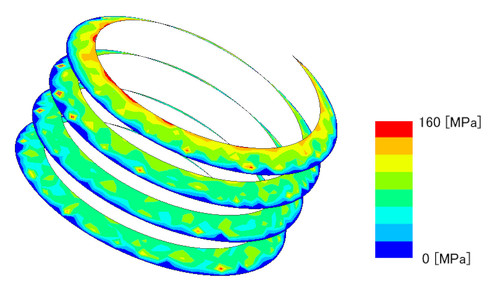
次は、選択すべき面圧の決定です。連載第4回でボルトの締め付けをシミュレートしていたのでこの結果を使います。おねじ山の面圧分布を図7に示します。
あれだけ細かく要素分割したのに面圧にばらつきが生じています。ばらつきの原因は参考文献[1]に述べられています。
参考文献:
- [1]日本機械学会:計算力学技術者1級 標準問題集:第6版(2009)
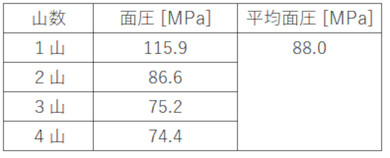
では、面圧の平均値を取りましょう。表2にねじ山の面圧の平均値を示します。シミュレーションでの締め付けトルクは22.29[Nm]で、M10ボルトのT系列による締め付けトルクは24.5[Nm]なので、シミュレーション結果を少し補正しています。面圧として1山目から4山目の面圧の平均値を採用し、88.0[MPa]とします。なお、先ほど示した図6の右端にある赤線部が88.0[MPa]の位置となります。
図6において、接触面圧が88.0[MPa]のときの摩擦係数を表3に示します。
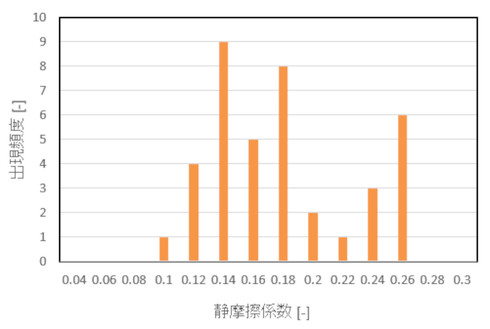
そして、図8が静摩擦係数の出現頻度となります。静摩擦係数は0.10〜0.26[-]まで分布しました。大きい摩擦係数の組み合わせを見てみましょう。「SCM435(クロムモリブデン鋼)−A5052(表面処理なし)」が0.259[-]でした。A5052が軟らかいので削られているのでしょうか。「SCM435(クロムモリブデン鋼)−SUS440」も0.259[-]で、今度は両者焼き入れ材でした。
機械の組み立てでは、ボルトを締め付ける際、ねじ山に潤滑剤やかじり防止剤を塗布しますが、それらを省略することも多いと考え、今回は“潤滑剤なし”で試験しました。いくつかの潤滑剤を使った場合の焼き入れ鋼同士の試験結果が報告されています(参考文献[2])。この文献による摩擦係数は潤滑剤なしで0.1〜0.4[-]程度、潤滑剤ありで0.1〜0.3[-]程度の値で、図8よりも少し大きなばらつき幅となっています。潤滑材があるとぐっと小さな摩擦係数となると考えそうですが、そのようなことはなさそうです。いずれにしても、摩擦係数はこの程度の範囲で大いにばらつくと考えた方がよいと思います。
設計に使用する摩擦係数
疲労破壊しない条件は、荷重作用時に締結面が離れないことです。このためには締め付け後のボルト軸力を見積もる必要があります。一般的に、ボルト締め付けトルクは呼び径とボルトの材質に対して決められており、被締結体(取り付けられる部品)の材質は規定されていません。つまり、どのような材質の部品でも同じトルクで締め付けられます。想定される材料が多岐にわたるということは、図8の全範囲の摩擦係数を想定しなければなりません。
連載第4回からボルト軸力Tは式1で計算されます。
μthはねじ山同士の摩擦係数、μbはボルト頭と被締結体との摩擦係数でした。摩擦係数が分母にありますので、摩擦係数が大きくなると軸力Tは小さくなります。どのような材質のめねじ部品や取り付け部品が来るのか分からないので、大きめの摩擦係数を採用しなければなりません。図8から、軸力Tを見積もるときの摩擦係数は0.26[-]としてはどうかというのが今回の提案です。
次回、締め付けトルクの決定について解説します。T系列が的を射た値であるかどうかと、自分で締め付けトルクを決める方法を述べます。このときの摩擦係数は0.26[-]ではなく他の値を使います。そして、軸力計算と締め付けトルク決定用のExcelシートを作ります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

![面圧88.0[MPa]のときの摩擦係数](https://image.itmedia.co.jp/mn/articles/2107/13/ay4328_teiketsucae05_hyo03_w590.jpg)
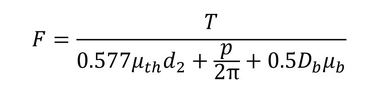 式1
式1





