独立の原則を頭に入れて測定したり、アセンブリーを設計したりする:3D設計推進者の眼(35)(2/5 ページ)
» 2018年11月30日 14時00分 公開
[土橋美博/飯沼ゲージ製作所,MONOist]
アセンブリーでの例題
これまで、公差計算・公差解析の私の話では、寸法(サイズ)公差のみを取り扱ってきました。以降は、以下のようなアセンブリーを例にして、幾何公差による公差計算・公差解析への影響を考えてみましょう。
3つの部品A,B,Cから構成されるアセンブリーです。管理したい寸法は、上図の赤丸で囲まれた隙間の寸法25[mm]となります。3つの部品A,B,Cは次のような寸法(サイズ)公差と幾何公差をしますが、ここでは、幾何公差の影響をシンプルに見るために、部品Bのみ幾何公差を設定します。
部品Bには、幾何公差として平行度0.1が設定されています。部品Bは、部品Aとの設置面をデータムCとしており、もう一方の部品Cの設置面に対してこの平行度0.1が設定されていることになります。
言い換えると、部品Bの上面(部品Bの部品Cの設置面)は、「独立の原則」から、寸法は、24.9[mm]から25.1[mm]の間でバラツキがあることと、その平行度公差域は0.1以内ということになります。
幾何公差の公差計算を考える時は、「平均的に部品の上面がある位置」を考えると私の先生であるプラーナーより教わっています。このことから、最も幾何公差範囲を満たすような形状となった場合(=最も形状の差異を生じていた場合)の設置面下図のような“傾き”を考えることができます。
端面から10mmの傾き量が0.05[mm]であったとき、端面から100[mm]の傾き量X[mm]はどうなるでしょうか。
10:90=0/05:X X=0.05×(90/10)=0.45[mm]
という簡単な計算で求めることができました。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
Special SitePR
あなたにおすすめの記事PR
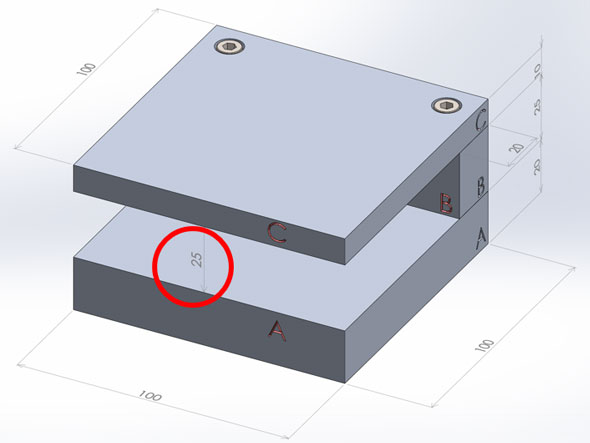 例1:アセンブリーモデル、不等角投影で表示
例1:アセンブリーモデル、不等角投影で表示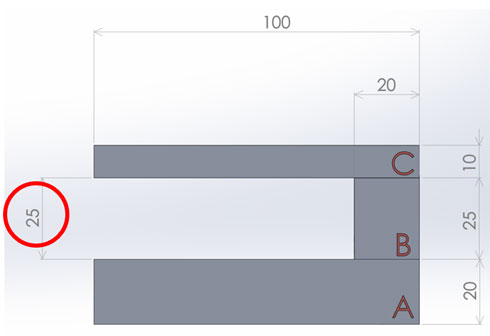 アセンブリーモデル、右側面で表示
アセンブリーモデル、右側面で表示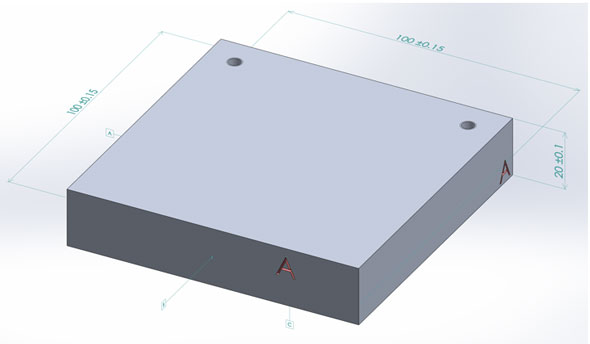 部品A
部品A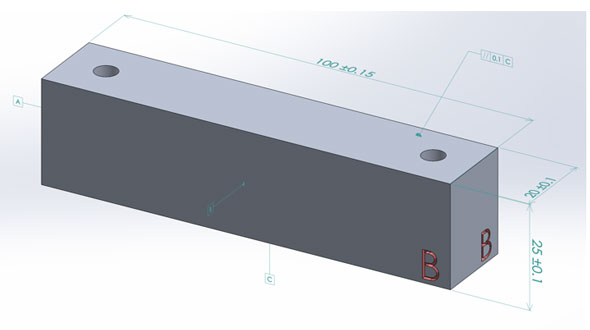 部品B
部品B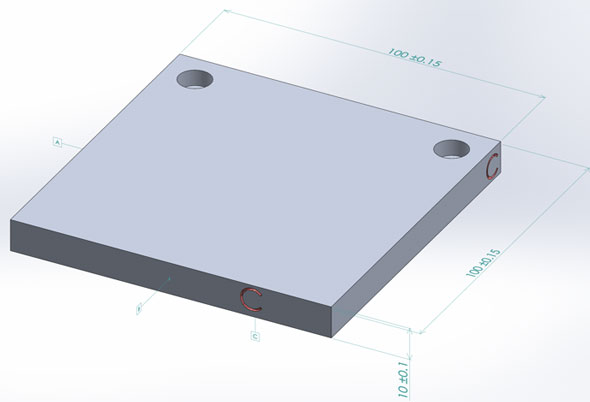 部品C
部品C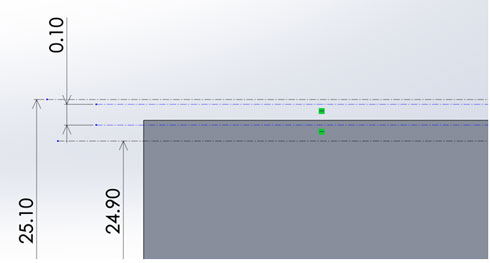 寸法(サイズ)公差値と幾何公差値のイメージ
寸法(サイズ)公差値と幾何公差値のイメージ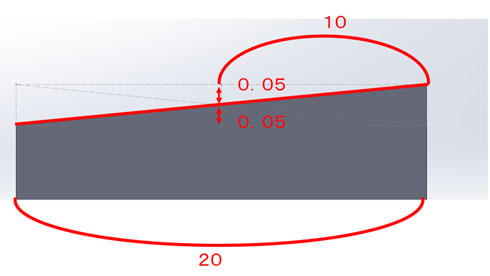 部品Bの部品C設置面(10倍表示)
部品Bの部品C設置面(10倍表示)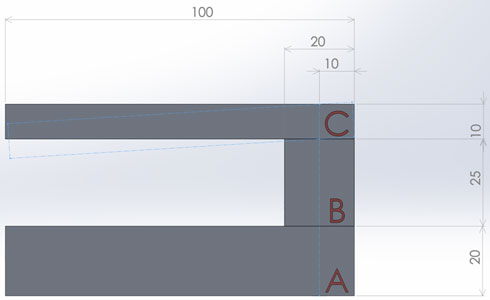 傾き量の拡大
傾き量の拡大





