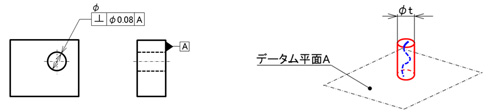幾何公差の本領発揮！ データムを使った姿勢公差と測定：寸法を実感する！ 測定講座（4）（2/4 ページ）

[木下悟志／プラーナー，MONOist]

直角度と平行度を姿勢公差として見たとき

　まず、直角度と平行度ですが、あえて説明することもないほどおなじみのものです。ここでは、幾何公差としてあらためて眺めた場合に特徴として見えてくる、中心形体に対する姿勢公差として注目します。中心形体とは、円筒軸や円筒穴の中心軸、または板物や切欠き形状の中心平面などがあります。前回のデータムの説明では、こういった中心形体をデータムにすることが非常に有効であると説明しました。同様に、直角度や平行度も中心形体に対して規制ができるのです。

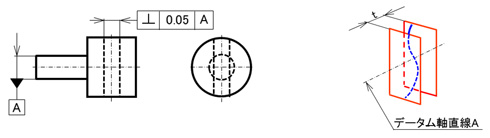
　図2は見慣れた外周面に対して直角度を指示した図例と公差域の説明図です。

図2：外周面に対する直角度指示と公差域

　図3が中心軸に直角度を指示した図例と公差域の説明図です。

図3：中心軸間の直角度指示と公差域

　この例では、データムも公差規制する形体も中心軸であり、慣れないと違和感があると思いますが、この事例は多く使われます。

　図4はさらに中心軸に対して方向性を示さず、直角度を指示した図例と公差域の説明図です。

図4：方向を示さない直角度指示と公差域

　ここで注目していただきたいのは、公差値にΦが付いていることです。公差域に注目して、図3との違いをご覧ください。図3のようにΦを付けない場合は、公差を示す寸法線の矢印の方向や関連するデータムに対する方向から公差域を想像する必要があります。その点でΦを使うと便利ですが、必要以上に過剰な公差指示をすることなく、本当に必要な方向を考えて公差指示を行うことは設計者に求められる重要な責務です。このことは、従来の寸法公差のみの図面では不明確なまま済まされていたことではないでしょうか。

　同様なことは平行度に関しても適用されますので、ここでは詳細説明を省かせていただきます。

直角度の測定方法

　直角度の測定ですが、正確には3次元測定機を用いて行います。しかし、現場レベルでは伝統的に直角定規（スコヤ）が用いられます。図5にその測定概念図を示します。

図5：直角度の測定方法

　この方法は意外に精度が高いのですが、さらに高精度で測定したい場合は、スキマゲージを用いずに光学的にスキマを測るか、スキマゲージを用いても正確に測る方法を考えます（詳細は割愛します）。いずれにしても、設計者は製造者、測定者との相談で、コストと時間をかけずに測定する方法を検討していくことが重要です。少なくとも、「測れないから精度を保証できない」という声に対して真摯に対応して行く努力が大切です。