統計の食わず嫌いを直そう(その8)、統計的に「王様の耳はロバの耳」と言うために:山浦恒央の“くみこみ”な話(80)(1/4 ページ)
「王様の耳はロバの耳」と統計的に判定するには、どうすればいいのでしょうか?ロバの耳かも?という仮説を“検定”するための基本的な考え方を学びます。
1.王様の耳はロバの耳か?
王様の耳がロバの耳であることを知った王様専属の床屋が、このことを胸にしまっておくのが苦しくて、ついに山へ行って穴を掘り、穴に向かって「王様の耳はロバの耳」と叫び、穴を埋めた……。有名なイソップ物語の寓話(オリジナルはギリシャ神話)ですね。
「王様の耳がロバの耳である」と統計学的に判定するには、「王様の耳がロバの耳であるという仮説が正しいかどうか『検定』し、正しい場合、王様の耳がロバの耳であると言える」となります。
今回も前回に引き続き、「検定」について解説します。新しいツールを導入したプロジェクトで生産性のデータを収集し、新ツールの効果を証明するには、データを収集して、検定しなければなりません。
2.母平均の差の検定
「検定」とは、2つのグループの母集団の平均に差があるか、確認する手法です。「王様の耳がロバの耳である」と判定するには、「王様一族の耳のデータ」の平均と、「国民の耳のデータ」の平均に差があるかチェックします。また、プロセス改善を実施し、差があると判定できれば、「効果がある」と言えるし、差が無ければ「効果無し」となります。
図.1に、前回示した「検定手順」を再掲します。以下、詳細な手順を示します。
2.1 仮説を立てる
統計学では、表.1のような仮説を設定します。
| 表.1 2種類の仮説 | |
|---|---|
| 仮説の種類 | 意味 |
| 帰無仮説 | 否定したい仮説(例:王様の耳は国民と同じ) |
| 対立仮説 | 採用したい仮説(例:王様の耳はロバの耳) |
表.1には2種類の仮説を示しました。統計学では、否定したい仮説と採用したい仮説を立てます。否定したい仮説を「帰無仮説(*1)」、採用したい仮説を「対立仮説」と呼びます。使い分けは、まず帰無仮説を立て、それを否定(*2)できれば、対立仮説が採用(*3)されるという仕組みです。よって、帰無仮説、「王様の耳は国民と同じである」を否定し、対立仮説、「王様の耳はロバの耳(ほど大きい)」が採用されれば、「王様専属の床屋」の判定は正しいと言えます。
実際に仮説を立てる場合、どうすればよいでしょうか。表.2に帰無仮説、対立仮説の立て方を記します。
| 表.2 仮説設定 | |
|---|---|
| グループAの母平均μ1, グループBの母平均μ2として考える。 | |
| 帰無仮説: | μ1 =μ2 (μ1とμ2 は等しいという仮説) |
| 対立仮説: | μ1 ≠μ2 (μ1とμ2 は異なるという仮説) |
| : | μ1 >μ2 (μ1の方が大きいという仮説) |
| : | μ1 <μ2 (μ2の方が大きいという仮説) |
表.2では、帰無仮説と対立仮説の立て方を示したものです。まず、帰無仮説と対立仮説を1つずつ設定します。対立仮説の立て方は、3パターンあります。どの対立仮説にするかは、場合によって目的によって異なります。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
- 1.5km離れた漁場をWi-Fi HaLowなどで可視化、海洋モニタリングの実証に成功
コーナーリンク

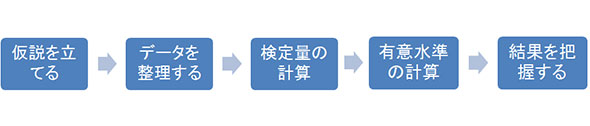 図.1 検定手順
図.1 検定手順

