ボード線図を使って過渡応答と周波数応答を求める:無償ソフトで技術計算しよう【制御工学応用編】(1)(2/3 ページ)
インパルス応答
インパルス応答とは、時間幅が無限小で高さが無限大のパルスを入力したときのシステムの出力です。
ある入力に対する応答は、(ラプラス変換後の)入力×伝達関数になります。ここで、インパルス信号、すなわちデルタ関数のラプラス変換は1であるため、伝達関数そのものがインパルス応答となります。インパルス応答を時間波形として求めるには、伝達関数にラプラス逆変換を施して、原関数を求めます。では、(1)式のラプラス逆変換を求めてみます。
【制御工学基礎編】(2)でも説明したように、(1)式右辺は下記のように書き換えることが可能です。
FreeMatは任意の次数の方程式を解くコマンドrootsを持っているので、これを用いて、インパルス応答の時間波形を求めるのが、ex507.mで、動作させると、図3に示すインパルス応答波形が得られます。
clear;m=1;c=1;k=10;
x=roots([m,c,k]);
t=0:0.1:20;
y=1/(x(1)-x(2))*(exp(x(1)*t)-exp(x(2)*t));
plot(t,y);grid('on');
インパルス応答波形を、伝達関数を微分方程式にして数値的に解くことで求めてみます。ただし、インパルス信号は、幅が無限小、高さが無限大の信号であり、数値的に実現するのは難しいため、代わりに、適当な初期値を与えて解いてみます。
まず、出力をYとすると、インパルス応答であるため、伝達関数が出力Yとなることから、(1)式を下記のようにします。
入力が0で初期値が0ではないとして、同様に、(1)式を下記のようにします。
ここで、(3)式と(4)式とが等しいならば、
が成り立ちます。
従って初期値は、
となり、入力を0として、変位の初期値が0、速度の初期値が1/mの微分方程式を数値的に解いたものがインパルス応答波形となります。
以上からインパルス応答を数値解法により求めるのが、ex508.mで、動作させると、図4に示す波形が得られます。
clear;m=1;c=1;k=10;
dydt=@(t,y) [y(2);(-c*y(2)-k*y(1))/m];
[t,y]=ode45(dydt,[0,20],[0;1/m]);
plot(t,y(:,1));grid('on');
伝達関数を微分方程式に変換する方法、微分方程式をFreeMatで数値的に解く方法については【制御工学基礎編】(3)を参照してください。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査
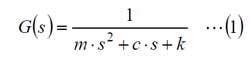

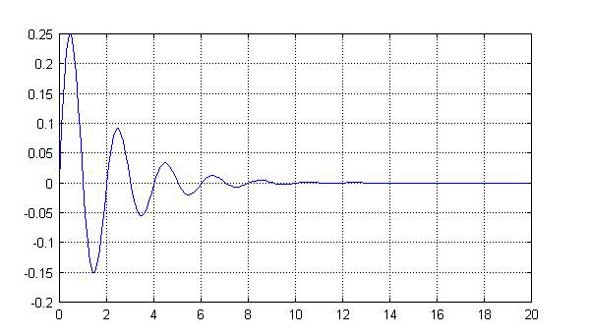 図3:伝達関数のラプラス逆変換により求めたインパルス応答波形
図3:伝達関数のラプラス逆変換により求めたインパルス応答波形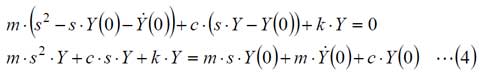
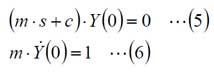

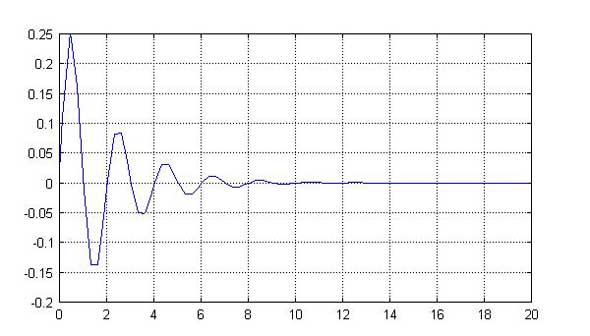 図4:数値解法により求めたインパルス応答波形
図4:数値解法により求めたインパルス応答波形





