ブロック線図を使ったPIDコントローラーのシミュレーション:無償ソフトで技術計算しよう【制御工学基礎編】(3)(1/3 ページ)
今回は、数式で表されたモデルを信号の流れとして可視化する「ブロック線図」と呼ばれる手法について説明する。
前回は、対象をモデル化する方法について説明しました。今回は、数式で表されたモデルを信号の流れとして可視化する「ブロック線図」と呼ばれる手法について説明します。
ブロック線図
ブロック線図は、図1に示すように、入力から出力までの信号の流れをブロックと線で表す手法です。
信号は矢印で左から右に流れるように描きます。左側の入力と書かれたブロックが、対象への入力で、前回の伝熱問題で言えば、周囲温度になります。ブロック線図では入力をUで表すことが多いです。中央のG1(s)と書かれたブロックが、対象の伝達関数で、伝熱問題では
の右辺となります。右側の出力と書かれたブロックは対象からの出力で、伝熱問題では物体の温度になります。ブロック線図では、出力はYと表すことが多いです。
信号を分岐させる場合は、図2に示すように、分岐する点に黒い点を付けて矢印を分岐させます。
信号を合流させる際は、図3に示すように、合流する箇所に○を描き、矢印を合流させます。合流する信号が加算される場合は「+」を、減算される場合は「−」を矢の箇所に付けます。
伝達関数の積は、図4に示すように直列接続となります。また、伝達関数の加算は、図5に示すように並列接続となります。
フィードバックループ
制御工学では、以上のルールに基づいてブロック線図を整理し、信号の流れを理解します。
例としてフィードバックループを作成してみます。制御では、結果が大きすぎたら、元の信号から差し引いて小さくするといった操作をして結果を安定化させます。これはフィードバックループと呼ばれ、制御の基本となります。前述の「元の信号から差し引く」という操作は、図6のようになります。
では、図6からフィードバックループの伝達関数を求めてみます。入力Uから出力YにG2を掛けたものが差し引かれるので、G1には、U-Y×G2が入力され、
G1×(U-Y×G2)が出力されます。これが出力Yと等しくなるので、下記の式となります。
となり、フィードバックループの伝達関数が得られます。
フィードバックループあるいはフィードバック型の伝達関数は図7に示すように、交互に置き換えることが可能です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
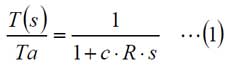
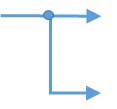 図2:分岐
図2:分岐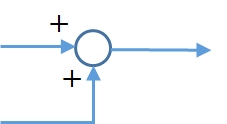 図3:合流
図3:合流 図5:伝達関数の並列接続
図5:伝達関数の並列接続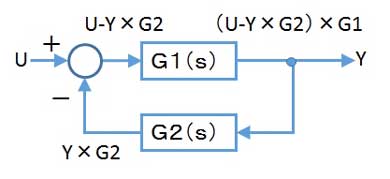 図6:フィードバックループ
図6:フィードバックループ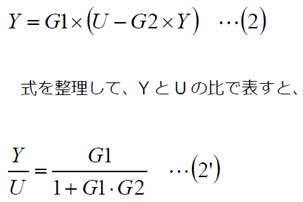
 図7:フィードバック型の伝達関数とブロック線図
図7:フィードバック型の伝達関数とブロック線図





