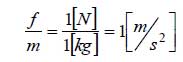振動問題をFreeMatで解いてみよう(その2):無償ソフトで技術計算しよう【シミュレーション応用編】(3)(1/3 ページ)
今回はバネ・マス・ダンパ系の方程式を無償ソフト「FreeMat」で解いてみる。
機械振動は、質量とバネ、減衰器との組み合せでモデル化できます。今回はFreeMatで、バネ・マス・ダンパ系の方程式を数値的に解いてみます。あわせて、振動対策についても説明します。今回紹介する例のように、装置の状態を表すモデル式をコンピュータ上で数値的に解いて、最適な条件を探索する手法は、モデルベースデザインと呼ばれ、近年、急速に普及しています(関連連載:モデルベース開発奮戦ちう)。
バネ・マス・ダンパ系
図1に示すバネと質量とダンパが組み合わせられたモデルを1自由度減衰振動モデルと呼びます。
自由度とは、状態が取り得る種類を表します。図1の場合、縦方向にしか動かないため自由度は1となります。図1の運動方程式は重力を無視すると、下記となります。
ここで、mは質量(kg)、kはバネ定数(N/m)、cは減衰係数(Ns/m)、fは質量に加わる外力(N)です。
下記の1階連立微分方程式になり、ode45で数値的に解くことが可能です。
バネ・マス・ダンパ系の数値解法
では、f=1(N)、m=1(kg)、k=10(N/m)、c=1(Ns/m)、初期条件は静止状態として、t=0〜10(s)での変位を解いてみましょう。
--> dydt=@(t,y) [y(2);1-y(2)-10*y(1)];
まず、このように方程式を定義します。
--> [t,y]=ode45(dydt,[0,10],[0;0]);
上のようにすると、yの1列目に変位、2列目に速度が格納されます。
--> plot(t,y(:,1));grid('on');
--> xlabel('Time[s]');ylabel('Displacement[m]');
さらに上のようにすると図2が得られます。
図2は瞬間的にmを上に引張上げた場合の振動の様子で振動が収まると、
となっていることが分かります。また、振幅の周波数は、図2で山から山までを読み取ると2秒であることから、1/2=0.5(Hz)となりますが、これは自由振動の周波数、
と一致します。
機械振動は加速度での表示が一般的です。
図2の結果を加速度で見るには以下のようにすると、図3に示すように加速度の変化が得られます。
--> a=ones(length(y),1)-y(:,2)-10*y(:,1);
--> plot(t,a);grid('on');
--> xlabel('Time[s]');ylabel('Acceleration[m/s2]');
引っ張り上げる瞬間の加速度は、以下のようになっています。
運動方程式に計算結果を入れれば、加速度が得られますが、その際、定数項も計算結果と同じ長さの配列(今回の場合は「ones(length(y),1)」)とします。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
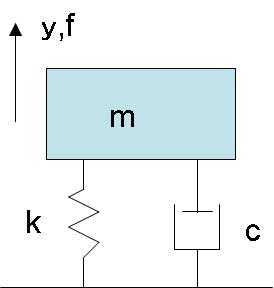 図1:バネ・マス・ダンパ系
図1:バネ・マス・ダンパ系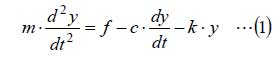
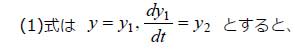
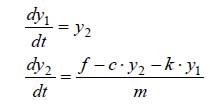
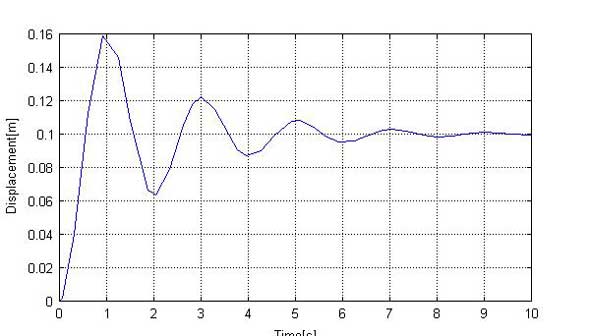 図2:変位の時間変化
図2:変位の時間変化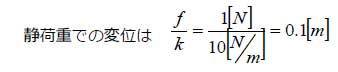
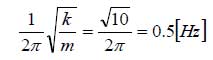
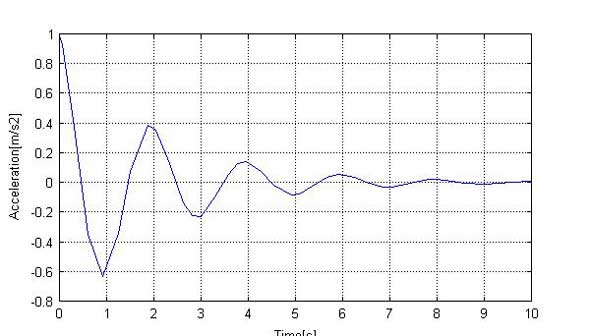 図3:加速度の変化
図3:加速度の変化