振動問題をFreeMatで解いてみよう(その1):無償ソフトで技術計算しよう【シミュレーション応用編】(2)(1/3 ページ)
今回は振り子の運動方程式や減衰振動を無償ソフト「FreeMat」で解いてみる。
» 2015年03月19日 10時00分 公開
[伊藤孝宏,MONOist]
今回と次回の2回にわたって振動問題をFreeMatで解く方法を説明します。
振り子の振動
振動問題の基本となる振り子について、運動方程式を導いてみます。図1に示す振り子の軌道に沿ってx座標を取ると、運動方程式は以下のようになります。
振り子の長さLと振れ角θとの関係から、x=L・θを用いると下記となります。
振り子の振れ角が小さい場合、sinθ≅θと見なせるので、(1)式は下記となります。
(2)式の一般解は、下記となります。
初期条件を例えば、t=0で、
として係数AとBを求めると下記となります。
周期は下記のとおりの振動となります。
以上は、振れ角が小さい場合には成り立ちますが、振れ角が大きくなると、sinθ≅θとは見なせなくなるので、下記の式を解く必要があります。
(1)式を解析的に解くことは大変な作業になるので、数値的に解いてみます。ちなみに、シミュレーション編の冒頭で紹介した図は、(1)式を数値的に解いたものです。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 設計者を支える3つのAI仮想コンパニオン 探索×科学×実現で製品開発を伴走
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 強度設計の出発点 “計算”より先に考えるべきこととは?
- NVIDIAとダッソーがCEO対談 産業AI基盤構築で戦略的パートナーシップ締結
- Subaru of America、3Dプリンタ用高速ヘッド導入でツール開発時間を50%以上短縮
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
Special SitePR
あなたにおすすめの記事PR
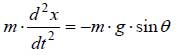
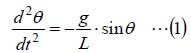
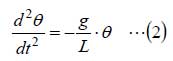
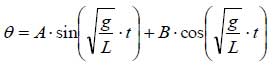
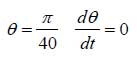
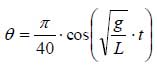
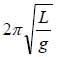
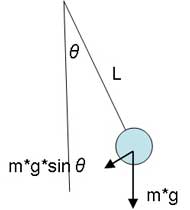 図1:振り子
図1:振り子






