振動問題をFreeMatで解いてみよう(その1):無償ソフトで技術計算しよう【シミュレーション応用編】(2)(2/3 ページ)
» 2015年03月19日 10時00分 公開
[伊藤孝宏,MONOist]
振り子の運動方程式の数値解法
ode45で(1)式のような2階の微分方程式を解くには、連立した1階微分方程式に置き換えて計算します。
つまり、
を下記のように書き換えます。
後は、(3)式と(4)式で示すθとφについての連立微分方程式を解けば、求める解が得られます。
では、g=9.8、L=1、初期条件をt=0で、
さらに解析区間がt=0〜10として、FreeMatで解いてみます。
始めに無名関数で連立微分方程式を定義します。
--> dydt=@(t,y) [y(2);-9.8*sin(y(1))];
ここでy(2)がφ、y(1)がθになります。次に、ode45にdydtと解析区間、初期条件を渡すと、配列yの1列目にθが、2列目にφが返ってくるので、y(:,1)として1列目のデータを指定してプロットすると、図2の結果が得られます。
--> [t,y]=ode45(dydt,[0,10],[pi/4;0]);
--> plot(t,y(:,1));grid('on');
カクカクした結果になっていますが、一定の周期となっています。これは、FreeMatのOde45が分割幅を比較的大きめにとるためです。参考までにMATLABで計算した結果を図3に示します。
カクカクした結果では見かけがあまりよくないので、解析区間を小さくして、区間の最後の結果を次の区間の初期条件として計算するようにしたのが、ex405.mです。図4に示す計算結果を見ると、滑らかになっているのが分かります。
dydt=@(t,th) [th(2);-9.8*sin(th(1))];
ts=[0,10];n=20;
tspan=linspace(ts(1),ts(2),n);
t0=[pi/4;0];
tt=[];theta=[];
for k=1:n-1
[t,th]=ode45(dydt,[tspan(k),tspan(k+1)],t0);
t0=th(length(th),:);
if(k<n-1)
t(length(t))=[];th(length(th),:)=[];
end
tt=[tt,t];
theta=[theta;th];
end
plot(tt,theta(:,1));grid('on');
ex405.m
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 設計者を支える3つのAI仮想コンパニオン 探索×科学×実現で製品開発を伴走
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 強度設計の出発点 “計算”より先に考えるべきこととは?
- NVIDIAとダッソーがCEO対談 産業AI基盤構築で戦略的パートナーシップ締結
- Subaru of America、3Dプリンタ用高速ヘッド導入でツール開発時間を50%以上短縮
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう
Special SitePR
あなたにおすすめの記事PR
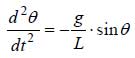
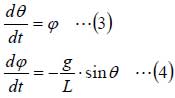
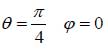
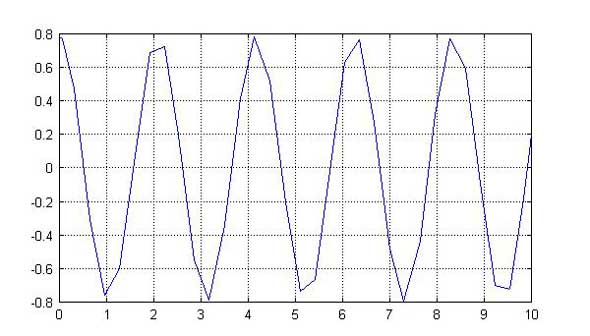 図2:振り子の運動方程式の数値解法結果
図2:振り子の運動方程式の数値解法結果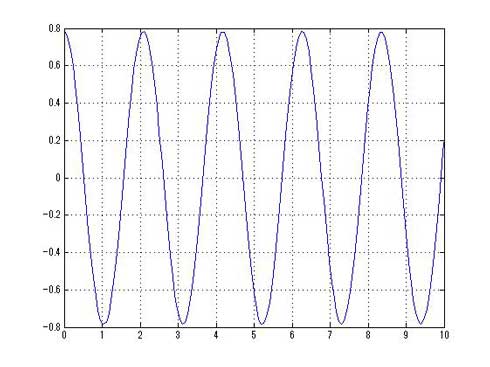 図3:MATLABで解いた結果
図3:MATLABで解いた結果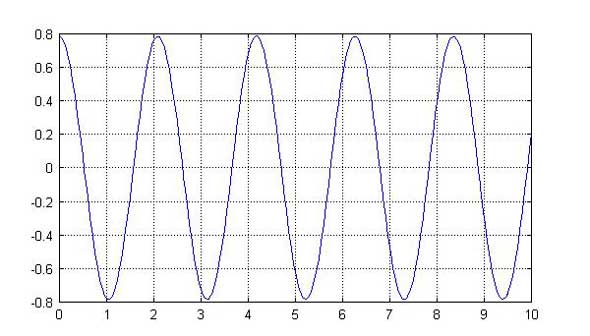 図4:振り子の運動方程式の数値解法結果
図4:振り子の運動方程式の数値解法結果





