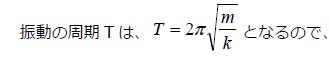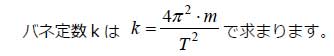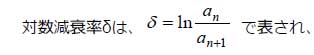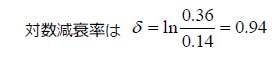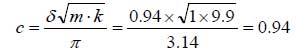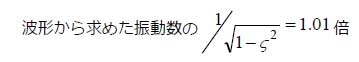振動問題をFreeMatで解いてみよう(その2):無償ソフトで技術計算しよう【シミュレーション応用編】(3)(2/3 ページ)
減衰速度
機械設計では、動いた後に速やかに停止してほしい場合があります。そこで、運動方程式のパラメータm、c、kを適当に変化させて、減衰の様子を見てみます。
分かりやすく、外力を与えずに、初期値を変位1(m)とします。また、パラメータを任意に変えられるように関数mファイルでプログラムを作成します。コマンドウィンドウ上でex407(1,1,10)などと入力し、subplotコマンドで複数の結果をプロットすると、図4に示す減衰波形が得られます。
図を見ると、減衰係数cを大きくすると、速く減衰することが分かりますが、質量mやバネ定数kを小さくしても、減衰が速くなることが分かります。
振動の減衰の速さは減衰比ζで表され、
式から、減衰比は減衰係数に比例する他、質量mやバネ定数kのルートに反比例することが分かります。
ただ、質量mは分かったとしても、バネ定数kや減衰係数cは分からないことが多くあります。そこで、停止時の減衰の様子が図5のようになったとして、これからバネ定数kと減衰係数cを計算してみます。
実際は測定結果のグラフから読み取ることになりますが、FreeMatで作成した図なので、ディスプレイ上にFigureウィンドウがでているうちに、コマンドウィンドウでt=pointと入力し、カーソルとFigureウィンドウに移動します。すると、カーソルが十字に変わるので、適当な山の位置でクリックすると、コマンドウィンドウ上に、時間t、変位yの順に数値が表示されます。同様に次の山でも繰り返し、2つの山の位置を測定します。
2つの山の時間情報からバネ定数を求めます。
質量mは測定済みで1(kg)として、2つの山の時間情報から、周期T=4−2=2(s)となり、バネ定数はk=9.9(N/m)となります。これは、モデルで設定したk=10(N/m)とほぼ一致します。
次に、減衰係数を求めます。始めに、図5から対数減衰率を求めます。
山と次の山あるいは、谷と次の谷の振幅の比の自然対数となります。
次に、減衰比ζと対数減衰率δとは、
対数減衰率δから、減衰係数cを求めることができます。では、減衰係数cを求めてみましょう。
2つの山のy座標は、0.36と0.14であったので、
となります。一方、質量mは計測済みで1(kg)で、図5から計算したバネ定数kは9.9(N/m)でしたので、
減衰係数cは、
となり、モデルで設定した減衰係数c=1(Ns/m)とほぼ一致します。このように、実験結果から、バネ定数k、減衰係数cが推測できれば、減衰振動モデルから、各種の対策の効果を数値解析により求めることが可能になります。
実は、説明の便宜上、区別をしていませんでしたが、上記で求めた振動の周期は、共振周波数であり、減衰がある場合、固有振動数とは異なります。従って、振動の周期から求めたバネ定数は、固有振動数から求めた値とは異なり、正確な値ではありません。では、どの程度異なるかを見積もってみましょう。共振周波数fsと固有振動数fとには、減衰比ζとの間に
従って、バネ定数を求めるための振動数、すなわち固有振動数は、
となります。
波形から求めた対数減衰率δ=0.94から減衰比ζを求めると、ζ=δ/2π=0.15となり、固有振動数は、
となります。
すなわち、波形から求めた周波数はおおむね固有振動数と等しく、求められたバネ定数は、おおむね正しい値と考えられます。実際、求められたバネ定数は9.9(N/m)とモデルに設定された値10(N/m)とほぼ同じ結果となっています。
function ex407(m,c,k)
dydt=@(t,y) [y(2);(-c*y(2)-k*y(1))/m];
[t,y]=ode45(dydt,[0,10],[1;0]);
plot(t,y(:,1));grid('on');
title(['m=',num2str(m),' c=',num2str(c),' k=',num2str(k)]);
ylabel('Displacement[m]');
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
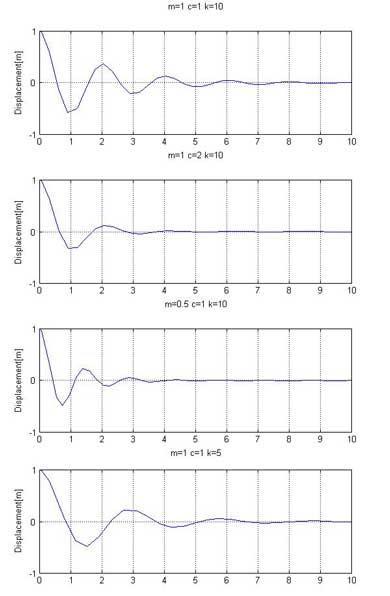 図4:パラメータの違いによる減衰の変化
図4:パラメータの違いによる減衰の変化
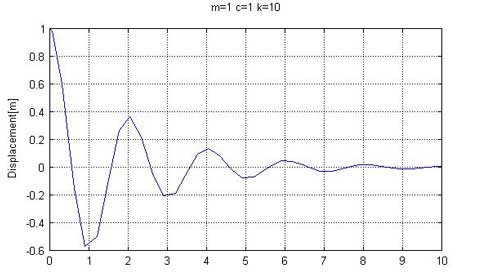 図5:減衰振動波形
図5:減衰振動波形