曲面と曲線、2種類の3次元グラフの描き方:無償ソフトで技術計算しよう【グラフィックス編】(3)(2/2 ページ)
3次元曲面プロット
グラフィックス編の最初で紹介した3次元グラフの作成方法について説明します。
3次元曲面をプロットするコマンドはsurfとcontour3の2種類があります。surf(x,y,z)では、曲面を表示し、contour3(x,y,z)では、等高線を表示します。曲面プロットで留意する点は、変数x,y,zは同じ要素数の行列を使います。これらの条件を満足する行列を作るにはいくつか方法がありますが、[x,y]=meshgrid([x変数範囲、y変数範囲])を使う方法が簡単です。具体的には、meshgridでx,yの格子を作成し、次にzを計算し、surfあるいはcontour3コマンドで描画するという手順になります。meshgridの働きを要素数の小さな例で見てみます。
これらをsurf(x,y,z);view(3);とすると、図4に示す右上がりの斜面ができます。
図4左は行列xを曲面に表示したもので、x=1〜5でyは一定の面となっています。一方、図4中央は行列yを曲面に表示したもので、y=1〜3でxは一定の面となっています。surf(x,y,z)というコマンドは行列xでx軸方向、行列yでy軸方向、行列zでz軸方向の指定しますが、x,y,zは、行列要素の位置で対応させています。例えば、x=1,y=1,z=2のプロットであれば、x(1,1),y(1,1),z(1,1)の要素をプロットしています。そのため、x,y,zは同数の要素の行列となります。
グラフィックス編 第1回の冒頭で紹介した3次元グラフ(図5)は、z=x*exp(-x^2-y^2)という関数をプロットしたもので、下記のex205.mで描画できます。
clear;
[x,y]=meshgrid([-2:0.1:2]);
z=x.*exp(-x.^2-y.^2);
surf(x,y,z);
xlabel('x');ylabel('y');
zlabel('x*exp(-x^2-y^2');
axis('equal');
view(3);
同じくcontour3は等高線を描画するコマンドで、contour3(x,y,z,等高線の数)とします。等高線の数は省略できます。ex205.mのsurf(x,y,z)をcontour3(x,y,z,30)に変更するだけで等高線表示に変わります(ex206.m)。描画される図を図6に示します。
clear;
[x,y]=meshgrid([-2:0.1:2]);
z=x.*exp(-x.^2-y.^2);
contour3(x,y,z,30);
xlabel('x');ylabel('y');
zlabel('x*exp(-x^2-y^2');
axis('equal');
view(3);
もう1つの例として、球体を表示してみます。球表面のx,y,z座標は、半径r、方位角az(0≦az≦2π)、迎え角el(0≦el≦π)で下記のようにパラメータ表示できます。
x=r*cos(el)*cos(az)、y=r*cos(el)*sin(az)、x=r*sin(el)
方位角azを行方向に要素を作成し、迎え角elは転置演算'で列方向に要素を作成します。すると、x,yはそれぞれ、迎え角の要素数×方位角の要素数の行列となります。zも同じ要素数とするために、ones(size(az))にr*sin(el)との積を取ります。このようにして出来上がったx,y,zをsurfあるいはcontourコマンドでプロットすると、図7に示すような球体が得られます(ex207.m)。
clear;
az=-pi:pi/50:pi;
el=(-pi/2:pi/50:pi/2)';
x=cos(el)*cos(az);
y=cos(el)*sin(az);
z=sin(el)*ones(size(az));
contour3(x,y,z,20);
axis('equal');
view(3);
◇
グラフィックス編は今回で終了です。お疲れさまでした。次の連載は「プログラミング編」ということで、FreeMatによるプログラムの作成について説明していきます。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング

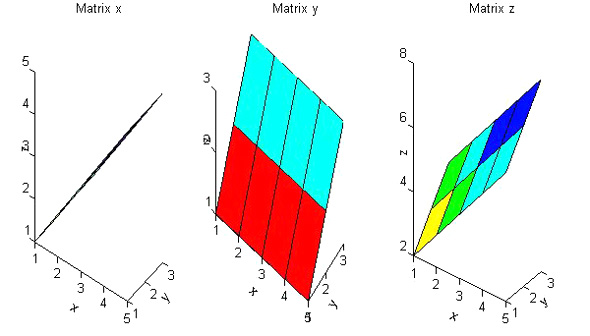 図4 行列x,y,zを曲面表示
図4 行列x,y,zを曲面表示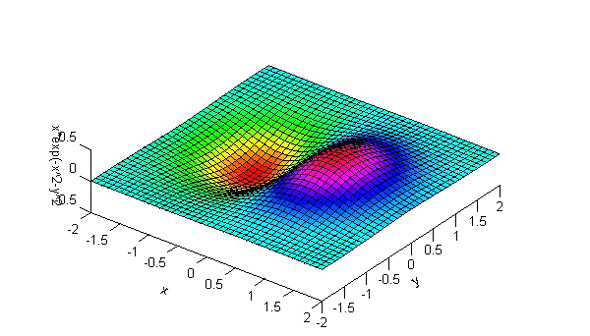 図5 曲面表示
図5 曲面表示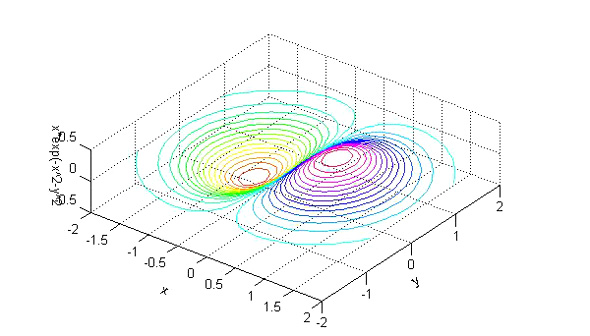 図6 等高線表示
図6 等高線表示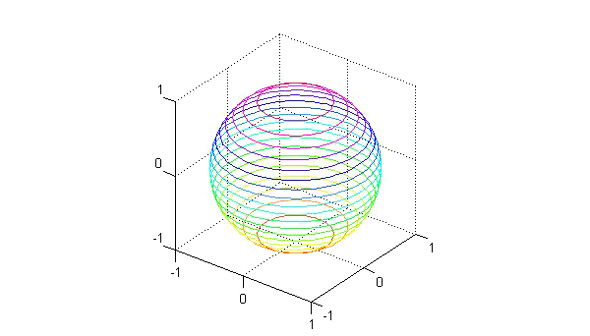 図7 球体
図7 球体






