静特性を取るか、動特性を取るか。それが問題や:独学! 機械設計者のための自動制御入門(11)(2/4 ページ)
そうか。分かった。まずステアリングGstの制御特性について説明しようか。ステアリングの制御は、図4のように制御部からハンドルをθh度回せ、という指令を受けて、モータがハンドルを回し、さらにピニオン-ラック機構を介してタイヤの操舵角をθs回転させる、いうものや。
モータが2つもあるね。
本当は制御部から直接ピニオン駆動モータの制御ドライバに、制御したい操舵角信号を入れてもいいんやけど、ハンドルを回した方がいかにも車を制御しているなって感じがするやろ。そのためにわざわざ、モータでハンドルを回してるんや。だから、ハンドル駆動モータ系の伝達関数は1と考えていい。
無人でハンドルが回るといかにも自動運転らしく見えるからね。もっともらしい構造にしたかったんだね。操舵角θsをピニオン駆動モータの制御ドライバにフィードバックしているけど、それはなぜ?
ハンドル角θhに対応する角度だけタイヤの操舵角も回転させるためにフィードバック構成にしたんや。そうせんと、ハンドル角が0でないときは操舵角は増え続けるからな。
ステアリングのブロック線図をピニオン駆動モータ系を中心に書くと図5となります。ここでVはモータ端子間の電圧、Rはモータコイルの抵抗、Lはインダクタンス、iは電流、Ktはトルク定数、Keは逆起電力定数です。モータは電流値iに比例してトルクを発生します。
このあたりについては、市販のモータ制御の本に詳しく書いてあるね。
そうや。モータは回転すると発電機になるやろ。すると逆起電力が発生してモータに掛かる電圧が下がる。だから速く回れば回るほど、トルクが出にくくなる。Iはモータ軸から見たタイヤを含めた機構全ての等価慣性モーメント、Nはピニオン-ラックのギア比だ。Gpはピニオン駆動モータを制御するための伝達関数。そしてκは、タイヤ操舵角とハンドル角との比で、ハンドル角1度がタイヤ操舵角κ度に対応している。
普通はインダクタンスLの影響は小さく、それを無視することが多いので、ここでも0とします。そうすると、図5の点線内の伝達関数は、
となります。つまり、点線のブロックは一次遅れ要素となります。さらに、図5のブロック線図を1つにまとめると、ステアリングの伝達関数Gstは
となります。モータのトルク定数Ktは逆起電力定数Keと同じものですから、Ktが、慣性モーメントIと抵抗Rと比べて大きければ、対応する逆起電力定数Keも大きな値となります。ですから、Gpを単純な比例要素とすれば、ある周波数以下では(2)は一次遅れ要素に近似することができます。
あるいは、ピニオン駆動モータを制御するための伝達関数Gpを一次進み要素、
としても、Gstは一次遅れ要素とすることができます。従って、図5は、図6のように単純化して書くことができます。
つまり、ステアリングの伝達関数は、一次遅れで表現されるんだ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- 製造業“現場あるある”かるた<あ行:結果発表> 秀逸作品ぞろいで審査難航!?
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 【レベル9】アセンブリ図面を作成せよ!
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 3Dプリンタ製の型を活用した、回せるネジ型チョコレートの取り扱いを開始
- 【調査レポート】設計・解析業務におけるAI活用の現実と課題
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 幾何公差の基準「データム」を理解しよう

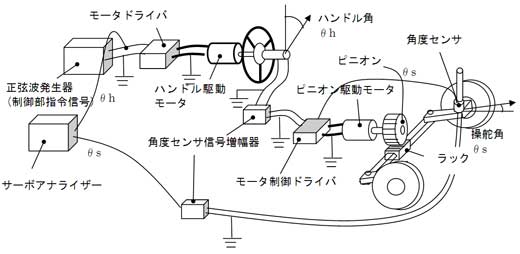 図4 ステアリングの周波数応答特性計測装置(再掲)
図4 ステアリングの周波数応答特性計測装置(再掲)
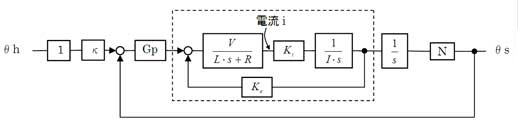 図5 ステアリング制御機構のブロック線図
図5 ステアリング制御機構のブロック線図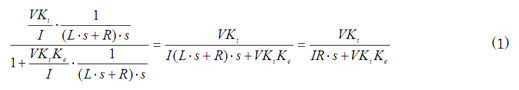
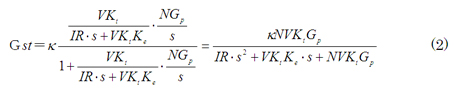
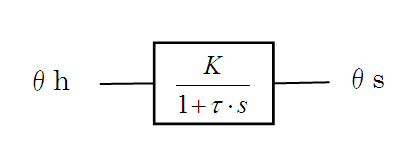 図6 単純化されたステアリングのブロック線図
図6 単純化されたステアリングのブロック線図





