OpenGL ESプログラミングで本格3D描画体験:“BREW”アプリケーション開発入門(7)(1/3 ページ)
OpenGL ESによる3Dグラフィックス描画プログラミングに挑戦! 投影、ライトなどの各種要素を理解し、立方体の描画を行ってみよう。
前回「はじめよう3D描画、BREWでOpenGL ESプログラミング」では、BREW環境でのOpenGL ESプログラミングの準備および、簡単な描画プログラムを紹介しましたが、今回はその続きということでもう少し3Dらしい描画について見ていきたいと思います。
なお、環境構築や初期化、EGLの設定などについては前回紹介したプロジェクトを流用することにして、省略して解説していきます。
今回の課題
今回は“3Dらしいグラフィックスを実現する”ということで、以下のような立方体を描画することを目的として、必要なOpenGL ESの各要素を見ていきたいと思います。
この中で、今回主に取り上げる要素は大きく以下の4つになります。
- 投影
- 視錐台の作成
- ライト
- カメラ
具体的な内容は各項目で解説しますが、3Dといえば行列計算などの数学的要素が出てくるのですが、ここでは3D数学などの話は割愛し、必要な要素について簡略化して紹介することにします。
3Dデータの準備
今回の描画対象となる3Dオブジェクトは立方体になりますが、最初に準備する3Dデータについて解説します。前回は単に平面の三角形(データ的には3Dですが)を描画しただけなのでイメージしやすかったかもしれませんが、今回は立方体を描画して、そこに3Dの効果を反映したり移動などを行うため、少しデータに対しての準備が必要になります。
まず立方体のデータを用意するに当たって、注意すべきことがあります。それはOpenGL ESは「三角形以上の多角面を描画する機能がない」ということです。そのため、立方体の1面の四角形を三角形で以下のように構成します。
つまり、三角形を2つ組み合わせることにより、四角形を構成するのですが、立方体は六面体ですので以上のような形状を6つ作ることになります。ここで気になるのが、頂点が重複している部分です。四角形単体の場合、頂点数は4つですが三角形を2つ使った場合頂点数は6つになり、しかも重複する頂点ができてしまいます。これでは効率性を考えるとあまりよろしくありません。そこで、OpenGL ESではこの三角形の描画に際して、データの効率化を行う「頂点インデックス指定」という手段が提供されています。これは指定された頂点からどのように三角形を描くかをインデックスで指定する方法です。これにより頂点数が少なくても三角形を以下のように描くことが可能になります。
そして、今回はライトによる光の効果を使いますので、「法線データ」を用意します。3Dグラフィックスにおける法線とは光の影響を受ける面のベクトルを表すものです。現実世界でも光に対して物体の面を動かすと見え方が変わりますし、人の目は光の反射によって物体や色を認識しています。これは3Dグラフィックスでも同様で、光の影響は非常に重要な役割を果たし、法線がないと光の影響を表現できません。
法線の情報は、面と点に対して付加できますが、ここでは比較的指定しやすい、点に法線を割り当てる方法で光の効果を得たいと思います。実際に指定する法線を図に表すと以下のようになります。
ここでは、光の反射が面に対して均一になるように立方体の各面の四隅に法線を配置しています。これは面法線を適用したものと同様の効果を得ることができる指定になります。
それでは、このデータをプログラムで確認します(今回は前回のプロジェクトにコードを追加する前提で話を進めます)。
boolean setupData(oes3d* pMe){
// 立方体の頂点データ(原点からの座標)
GLbyte _vertices[] =
{
-5, 5, 5, 5, -5, 5, 5, 5, 5, -5, -5, 5, // 正面
-5, 5, -5, 5, -5, -5, 5, 5, -5, -5, -5, -5, // 背面
-5, -5, 5, 5, -5, -5, 5, -5, 5, -5, -5, -5, // 下面
-5, 5, 5, 5, 5, -5, 5, 5, 5, -5, 5, -5, // 上面
5, -5, 5, 5, 5, -5, 5, 5, 5, 5, -5, -5, // 右面
-5, -5, 5, -5, 5, -5, -5, 5, 5, -5, -5, -5 // 左面
};
// 立方体のインデックスデータ(結線情報)
GLubyte _indices[] =
{
0, 3, 1, 2, 0, 1, // 正面
6, 5, 4, 5, 7, 4, // 背面
8,11, 9,10, 8, 9, // 下面
15,12,13,12,14,13, // 上面
16,19,17,18,16,17, // 右面
23,20,21,20,22,21 // 左面
};
// 法線データ
GLbyte _normals[] =
{
0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, // 正面
0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, // 背面
0, -1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, // 下面
0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, // 上面
1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, // 右面
-1, 0, 0, -1, 0, 0, -1, 0, 0, -1, 0, 0 // 左面
};
// データ保持のためのApplet構造体にコピー
MEMCPY(pMe->m_Vertices, _vertices, sizeof(_vertices));
MEMCPY(pMe->m_Indices, _indices, sizeof(_indices));
MEMCPY(pMe->m_Normals, _normals, sizeof(_normals));
if ( IGL_glGetError (pMe->m_pIGL) != GL_NO_ERROR ){
return FALSE;
}
return TRUE;
}
| ソース1 |
さらに、関数宣言とApplet構造体にメンバも追加します。
boolean setupData(oes3d* pMe);
// 立方体描画用 GLbyte m_Vertices[72]; //立方体の座標 GLbyte m_Normals[72]; //法線情報 GLubyte m_Indices [36]; //インデックスリスト
ここでは、単にデータを設定しているだけですが、3つのデータはそれぞれ前述した要素を持つものになっています。頂点データは立方体の頂点のデータを格納したもので、x、y、zの座標データが入っています。この座標系はコンピュータの3D空間における位置を示す「ワールド座標」と呼ばれます。ここでは、3D空間全体の中の位置を示すものであると考えてください。その原点(0,0,0)からの相対位置をここでは指定しています(この位置に特に意味はなく、仮として場所を決めているだけです)。また、法線も座標が示されていますが、z値しか値を持っていません。これは、法線が対応する頂点のz軸に対してのベクトルしか持たないためです。そして、インデックスデータは各頂点がどのように三角形を構成するかを示す情報です。ここで指定されている情報は、頂点データが格納された配列の要素数を示しており、例えば正面に対しては、以下のように三角形が描かれることになります。
以上のように頂点座標は4つしかありませんが、インデックスの指定により三角形が描かれます。この際に注意してほしいのが、OpenGL ESのデフォルトではこのインデックスの指定を“反時計回り”に行うということです。配列内の頂点データの並びは特に決まりはありませんが、頂点データの配列を視野に入れてインデックスの指定を考える必要があります。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- 1.5km離れた漁場をWi-Fi HaLowなどで可視化、海洋モニタリングの実証に成功
コーナーリンク
 図1 今回の描画対象となる3Dオブジェクトのイメージ
図1 今回の描画対象となる3Dオブジェクトのイメージ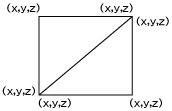 図2 立方体の1面の四角形を三角形で構成
図2 立方体の1面の四角形を三角形で構成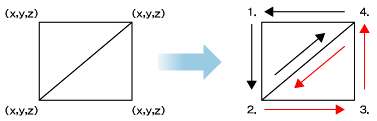 図3 頂点インデックス指定で描画
図3 頂点インデックス指定で描画 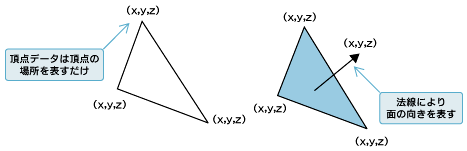 図4 法線について
図4 法線について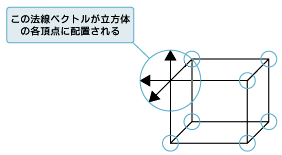 図5 法線を図に表す
図5 法線を図に表す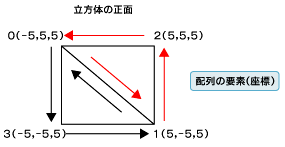 図6 立方体の正面
図6 立方体の正面

