　例えば、因子の数5、各因子の水準の数2の製品評価実験を、要因実験に基づき実施するとなると、実験の回数（＝試作品の数）は32回（＝2×2×2×2×2）になります。実験の回数が増えると、時間とコストの増加といった問題だけでなく、実験の条件が均一に保てなくなり、精度が悪化するといった問題が発生します。どちらにせよ、実験の回数は少ないに越したことはありません。

　このような現場の状況、ニーズに対応するため、すべての組み合わせではなく、一部の組み合わせのみの実験で、因子の効果を評価する方法が考案されました。この方法は、一部実施法と呼ばれ、今回のテーマ、直交配列実験は、一部実施法に含まれる手法の1つです。ほかには、ラテン方格実験と呼ばれる方法があります。

　方法の詳細は、後で説明いたしますが、直交配列実験の方法を利用すると、先の因子の数5、各因子の水準の数2の製品評価実験の実験回数32回を8回に減らすことができます。すなわち32個作らなければいけなかった試作品の数を8個に減らすことができるのです。

直交配列実験

　実験の手順は大きく、

実験の計画
実験の実施
実験データの解析

の3段階に分かれます。直交配列実験の方法が関与するのは、1と3です。2に関しては、精度の高いデータが収集できるよう実験を実施してください。次に、1と3の詳細を解説します。

1. 実験の計画

直交表の選択

　直交配列実験の計画は、直交配列表と呼ばれる表を利用して実施します。直交配列表とは、因子の水準の組み合わせをまとめた表で、実験の対象となる因子の数や水準の数に対応して複数の表が準備されています。直交表は図1のような記号で表現され、記号に示された数値を見て、複数ある直交表の中から、実施しようとしている実験の条件に合った直交表を選択します。

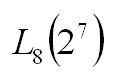図1　直交表の表記例
記号の意味（左から）L ：ラテン方格法の頭文字のL
8：その直交表で実験を計画した場合に実施する実験の回数
2：実験に取り上げる各因子の水準の数
7：その直交表で取り上げることができる因子の数の最大数＋1（要するに、この数値から1引いた数がその直交表を使って取り上げることができる因子の最大数）

　例えば、因子の数5、各因子の水準の数2の実験計画に直交表を利用する場合、

「右上の数値-1」が5以上になっている
「真ん中の大きな数値」が2になっている

直交表を選択します。この場合、先に例で示したL₈(2⁷)直交表が条件を満たし、この直交表を選択することになります。Lは、すべての直交表で共通です。このLは、直交配列実験の方法が、ラテン方格法をベースに考案されたことを意味しています。また、直交表の記号は簡素化してL₈などと表現される場合があり、L₈のほかによく利用される直交表としてL₁₆やL₃₂があります。