摩擦があると、どうしてエネルギーを失うのか:ピタゴラスイッチの計算書を作ろう(1)(3/3 ページ)
ニュートンの運動方程式と力学的エネルギーの保存則と段差Hs
摩擦によって力学的エネルギーが損失することを理解するためには、ニュートンの運動方程式をきちんと理解する必要があります。
銀二「ニュートンの運動方程式を書いてごらん」
草太「はーい。a を加速度、m を質量、Fを力として……」
銀二「それじゃ、まるで中学生だよ。大学生なんだから、微分方程式で書けるだろう。図1.4に示す斜面に置かれた矩形物についてニュートンの運動方程式を書いてごらんよ」
草太「えっと……、矩形物が動く速度を v とすると、こうか(1-8)´」
銀二「じゃあ、図1.4のように、x軸を斜面に沿って取り、y軸を斜面に垂直な方向に取って運動方程式を書いてごらん」
草太「まず、物体に作用する力は重力mg だな。斜面に平行なx軸方向についての運動方程式は、斜面に沿って動く速度をvx とすると……」
草太「次に斜面に垂直な方向の運動方程式は、速度をvyとし、物体が斜面から受ける力をN とする」
草太「しかし、N が分からない……」
銀二「物体は斜面に拘束されてx軸方向には運動できてもy軸方向には運動できない」
つまり、
銀二「摩擦を考えていないね。摩擦係数をμとすると、物体の動く方向とは反対方向にμNの力が作用するから(1-9)は、こうだ」
銀二「(1-12)の左辺と右辺だけを抜き出して書き直そう」
銀二「ここから面白いテクニックを紹介するから見ててごらん。 (1-13)の両辺にvxを掛けるよ」
銀二「物体が斜面に沿って移動した量をxとする」
銀二「だから、(1-14)の右辺のvx を(1-15)で置き換えると……」
銀二「さらに(1-16)の両辺のdt を消去する」
銀二「これを図1.5の地点1から地点2まで積分する」
草太「積分か。面倒くさいな」
銀二
「この程度の積分が分からないなら、技術者として生きるのをやめた方がいいぞ。 微分・積分が出てきたら『もうお手上げっ!』っていう人は結構多いけれど、積分は微分の足し算だから、極限の概念を除けば小学生でも理解できるはずなんだ。微分・積分なんて掛け算、割り算と同じで使わないから忘れるだけなんだよ。本当はその辺りの話もしたいけど、今回は止めておこう。そのうち、教えてあげるよ」
草太「分かりました。いつかお願いしまーす……」
銀二「従って、図1.1の曲線スロープのA地点からB地点まで積分すると 」
草太「あれ? x がs に変わっているよ?」
銀二「図1.5では直線的な坂に沿ってx 軸を取っていたけど、曲線スロープの場合は曲線に沿った座標軸を選んでいるので、x をやめ、s としたんだ。曲線をいくつかの直線に分けて考えてみると分かるけれど、(1-19)の右辺の第1項の積分は段差Hsとなるね」
銀二「図1.6と積分の定義を考えれば 、こうなるのは分かるだろ?」
銀二「だから(1-19)は、こうだ」
もし摩擦係数μが0、つまり摩擦がなければ、力学的エネルギーが保存されます。しかし現実に摩擦は必ず存在するので、左辺の第2項が存在し、B地点でのエネルギーがその分だけ損失します。
銀二「草太が最初に書いた(1-1)は(1-21)に対応しているのが分かるだろう。力学的エネルギーの保存の関係は、こうやってニュートンの運動方程式から導かれたものなんだよ」
(1-21)式と見比べてみましょう。
草太「なるほど。 (1-21)の左辺の第2項が(1-1)のエネルギー損失Elossなんだね。この摩擦による損失エネルギーの大きさは摩擦係数μに関係するから、傾斜を滑る物体の材質によって変わってくる。そして、これが計算できれば、B地点で欲しい速度に対して、必要な段差Hsを計算で求めることができる。摩擦係数μが大きいと損失も大きいということだね」
銀二「そういうのを、早とちりっていうんだ……」
草太「なんでよ!」
銀二「図1.4や図1.5は矩形物が滑り落ちる場合だろ? ピタゴラスイッチの場合はボールだぜ(図1.7)」
草太「おっとそうだった。でも考え方は同じでしょ?」
銀二「同じだといえば同じだし、違うといえば違うね。ボールは球だから転がるだろ。滑らずに転がったり、滑ると同時に転がる場合もある」
球の場合には、回転運動についても考えなければなりません。図1.7は、ボールが斜面で運動するときの力の状態を示していますが、回転角速度ωが新たに運動の変数として入ってくることが分かります。このことは(1-2)でも説明していますが、損失エネルギーElossの計算も回転の影響を考えなくてはいけません。
◇
銀二「おお! もうこんな時間だ。新幹線の発車時刻に間に合わなくなる。実は、今晩カミサンと神戸でデートの約束があるんだ。悪いけど、続きはまた今度にしよう。じゃあな、アディオス!」
草太「叔父さん! ちょっと、今度はいつ来るのーっ!」
次回は、具体的にサブシステム1の曲線スロープの設計をしながら、ボールの材質選定が重要であることを説明し、さらに実験検証によって、そのことを確認します。(次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞

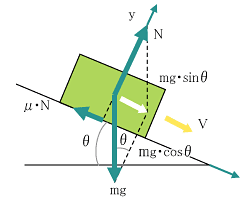 図1.4 矩形物の斜面の運動
図1.4 矩形物の斜面の運動 
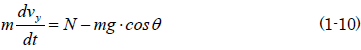
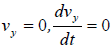
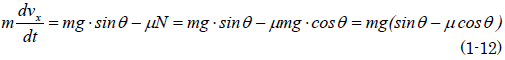

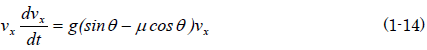

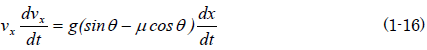
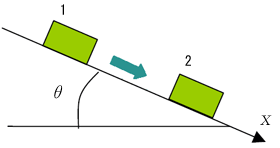 図1.5
図1.5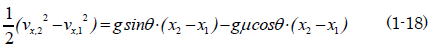
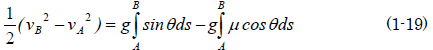
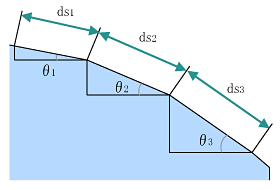 図1.6 曲線を直線に分解する
図1.6 曲線を直線に分解する 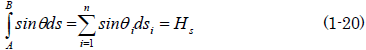
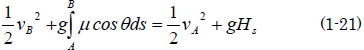
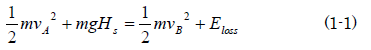
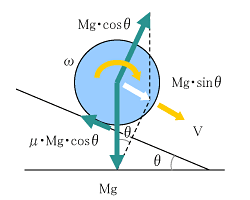 図1.7 ボールの斜面の運動
図1.7 ボールの斜面の運動






