台車を狙いどおりに転倒させるよう計算しよう:ピタゴラスイッチの計算書を作ろう(4)(1/4 ページ)
台車が直線スロープを降り、ストッパと衝突したときにきちんと転んでほしい。 さあ錘(おもり)の重量はどれくらいにしよう?
ロック機構の設計
いよいよ台車の設計に入ります。サブ・システム2のゲートを通過したボールが、台車を繋留していたロック機構を解除した後、台車は直線スロープ2を一気に滑り落ちます。台車はストッパと衝突して回転し、台車の中のボールが落下します。
草太「今度はロック機構の設計だね。設計条件はなんだろうね」
銀二「ゲートを通過したボールが確実にロック機構を解除しなければ駄目だ。そのためにはゲートを通過したボールの軌跡を把握しておく必要がある」
草太「僕がやった実験では、ベニヤ板のゲートなら、ボールはきれいにゲートを通過していたけどなぁ」
X年度 卒業設計課題(亜津戸大学 工学部 物田研究室)
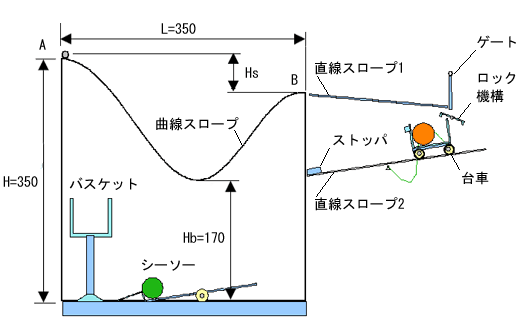
図のようなピタゴラスイッチを設計・製作し、設計計算書と試作品を提出せよ。
A地点から出発したボールは曲線スロープを経てB地点に到達し、直線スロープ1の終端のゲートを通過した後、直線スロープ2に繋留(けいりゅう)している台車のロックを解除する。
繋留が解除された台車は直線スロープ2を降り、ストッパによって横転し、台車の中のボールがシーソーに落下して、反対側のバスケットボールを跳ね上げ、バスケットの中に入るものとする。
なお、曲線スロープの出発地点Aの高さHとスロープの底の高さHb、曲線スロープの長さLは図示した値とし、また、B地点を通過するときのボールは極力遅くなるように設計すること。
銀二「草太がやったのは、直線スロープ1の始点Bから速度0で落下させたときの場合だろ? 実際には、曲線スロープから登ってくるボールは、曲線スロープの終点=直線スロープ1の始点=Bで速度が0とは限らないから、ゲート衝突するときはもっと勢いがある。前回の検討では最速837mm/sでBを通過する可能性がある。その場合には、草太がやった実験のような軌跡となるとは限らんよ」
草太「サブ・システム1の曲線スロープはもう作ってあるから、サブ・システム2につないで、実際にやってみれば分かるんじゃないの?」
銀二「それでは、設計にならんだろう。設計は本来机上で行うものだ。そうはいってもすべてが机上で設計できるはずもないから、不明な部分については実験データを使って設計することもある。最初から実験に頼っていると、いつまでたっても実験しなけりゃ設計できない、ってことになる。それでは進歩はない」
草太「じゃあ、念のためシミュレーションで確認してみようよ」
直線スロープ1の始点Bからボールを落下させたとき、速度0のときと速度837mm/sのときのシミュレーション軌跡を図4.1に示します。
草太「思ったほど差がないね。直線スロープ1の終端から20mm下の位置で、水平方向に約5mmしか軌跡に差がないね。この差を吸収できるようにロック機構を設計すればいいんだ」
銀二「思ったより差が出なかったな。837mm/sで落下させたときの軌跡はゲートと衝突した後上に跳ね上がっているな。これはボールの回転の影響だな」
草太「速度が速いということは同時に回転も速いからゲートに衝突したときに回転方向に跳ね返ろうとしているんだ。ビリーヤードで回転を掛けたときの球と一緒の動きだね」
銀二「じゃあ、設計したロック機構を作……」
草太「叔父さん。この前出した僕のメールでも『ロック機構と台車は先に作っとくよ』って書いたじゃない。もう作っちゃったんだよね」
草太「これ(写真4.1)がロック機構で、これが台車(写真4.2)。そして直線スロープ2の傾斜角度は10度。直線スロープ1の傾斜が5度だったからその2倍としてみたんだ」
草太「台車の中に入れるボールは、曲線スロープで使ったスーパーボールと一緒に買った中で一番重いボールを使おうと思っているんだ。それから、図1.1では、スロープからのボールが当たってロックが外れ、その後のボールの行方は知らん、というイメージだったけど、僕は網で受ける構造にしたよ。その方が、バトンリレーみたいでいいでしょー」
銀二「仕事をしてくれたボールを放っておくんじゃなくて、『ねぎらいと感謝の意味を込めて、網で受け取る』、そんな感じかな。それが草太の設計センスなんだね。じゃあ、草太の設計を評価してみようか」
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 品質はどのように作られ、どのように確認されているのか
- ソフト設計者が混乱する機械屋からの要望【安全対策編/前編】
- 加工不備や配線不良、バッテリー不具合、熱問題 品質課題が顕在化した1月のリコール
- パナソニック コネクトがSnowflakeのAI機能を活用し、設計仕様の照合作業を9割短縮
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 超小型EV「mibot」開発に見る“制約を魅力へ変える”設計アプローチ
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 3Dプリントによる格子構造を利用した枕のクラウドファンディングを発表
- 幾何公差の基準「データム」を理解しよう
- 3σと不良品発生の確率を予測する「標準正規分布表」
 ピタゴラスイッチ
ピタゴラスイッチ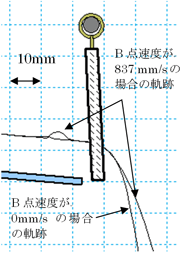 図4.1 ボールの軌跡
図4.1 ボールの軌跡 写真4.1 ロック機構
写真4.1 ロック機構  写真4.2 台車
写真4.2 台車





