台車を狙いどおりに転倒させるよう計算しよう:ピタゴラスイッチの計算書を作ろう(4)(3/4 ページ)
反発係数を正しく理解しよう
銀二「反発係数の式は、衝突点に対して成立する。(4-6)は反発係数の式を重心速度に対して適用しているから間違いだ。まず、草太は衝突点を支点として台車が回転すると思い込んでいるけど、そうなるためには条件が要るんだ」
右の図4.5で説明しましょう。台車が速度vbでストッパに衝突すると、衝突点Cには衝突反力f が発生します。衝突点Cでの台車の衝突直前の速度vc,b=vbは台車が走ってきた方向に反発速度vc,a=e・vc,bで跳ね返されます。このとき重心を回転中心とした回転モーメントs・f により台車には回転力が発生します。
次に、台車の重心Gから見た台車の衝突点速度について考えてみましょう。衝突後の速度vc,aを衝突点Cと重心Gを結んだ直線CG方向成分と、CGと直角方向成分に分解してみます。CG方向成分は台車の衝突点が台車の重心に向かって跳ね返る速度で、CG直角成分は重心Gを中心に衝突点が回転するときの周速度です。台車が剛体だとすれば、台車の重心速度は反発速度vc,aのCG直線上の速度成分と同じになります。つまり、台車の重心Gは、その速度でCGの方向に跳ね返されることになります。
このようにしてCGと直角方向の速度成分は先ほどの回転モーメントによって引き起こされます。従って、台車の衝突点Cは、衝突する前の方向にそのまま跳ね返り、台車の重心Gは回転しながらCG方向に飛ばされる、という運動をすることになります。
銀二「衝突点が回転の支点となるためには、衝突後の台車は跳ね返されては駄目だ。だから、台車とストッパ間の反発係数は0でなければならない。0にできなくても、なるべく小さい反発係数とすることが大事だ。幸い、草太は軟らかい木材でバンパーを付けているからその点はOKだ」
草太「ストッパはアクリル板で硬そうだったから、衝突のショックを和らげるつもりで木製バンパーを付けたんだ。転倒させやすくさせるためになんて考えもしなかったよ」
銀二「試行錯誤でものづくりをすると、たとえうまくいったとしても、うまくいった理由が分からないまま進んでしまう。ここに思わぬ危険が潜んでいるんだ」
草太「えー。うまくいけばいいんじゃないの?」
銀二「理屈が分からず作った機械は、設計変更も安易にしがちだ。コストが低くなるという理由で部品材質を変えたら、トラブルが発生して、その対策のために経費が発生して逆にコスト高となったというのはよく聞く話だ」
草太「なるほどね。ところで反発係数というのは衝突点で定義されているんだね。バンパーの反発係数が0なら、衝突点の台車の速度は0。台車は衝突点Cを中心として回転する。では、台車の回転速度はどうなるんだろうか?」
銀二「衝突点Cでの衝突方向の衝突後の速度は0だけど、衝突によって台車には回転モーメントが作用するから台車は回転する。すると図4.6に示すように、衝突方向と垂直方向にも衝突力Fyが発生する。つまり衝突方向の衝突力Fxと回転によって誘引されるFyによって台車の重心G にはそれぞれの速度vx,vyが発生するんだ。これらの速度は回転によって引き起こされるからこれらの速度が分かれば回転速度を計算することができる(図4.6)」
草太「そうか! 衝突直後の重心G の並進速度や回転速度はそれぞれの運動方程式を立てれば求めることができるんだったね」
そういうと草太は、ノートに計算式を書き始めました。そして、台車が転倒する条件式を求めました。
草太の解答例は、4ページ目にあります。
草太「結局台車が転倒するための条件は、衝突点C周りの慣性モーメントをJcar_cと書くと、こうなるね」
銀二「ブラボー! すごいな、よく分かったな」
草太「前回学んだことを利用しただけだよ。えへへ」
草太は、台車が転倒するかどうか確認するために、Excelで具体的に計算しはじめました。
草太「やっぱり、このままでは台車は転倒しないね。理論上も錘を付ける必要があるということがはっきりしたね。なるべく軽い錘でも転倒するように錘の取り付け位置は前方でかつ高い方がいいよね」
2人は、急きょ、針金を使って錘が取り付けられる部品を作成しました(図4.7)。そして草太は、台車が転倒するために必要な錘の重さを、再びExcelで計算して求めてみました。草太の計算によれば15.2gの錘を付ければよいということが分かりました。これらの具体的な計算内容を紹介しておきます。
草太の計算内容は、4ページ目にあります。
銀二「そうだね。草太が計算した式(4-20)を使えば、どの程度の錘を付けたら転倒するかが分かるな。ただし、草太の説明した理論は台車とストッパの構造を単純化した場合であって、実際はもっと複雑だ。特に今回はボールが入っているからさらに複雑の度合いが増している。台車がストッパと衝突すると台車は一瞬停止する。すると同時にボールは台車に衝突することになる。まともに、台車の運動を解析しようと思うとかなり複雑な連立微分方程式を解くことになるよ」
こうなると手計算で精度の高い運動解析行うことはほとんど不可能です。しかし、いまの時代にはシミュレーションという有力な武器があるのです。シミュレーションを行い、その結果と草太の計算結果とを比較してみましょう。
シミュレーションの活用
銀二叔父さんは草太のパソコンを使って、草太にシミュレーションのやり方を指導し始めました。シミュレーションのモデリングは思ったほど難しくなかったためか、草太は夢中になってやり始めました。
銀二「じゃあ、お前の作った台車で転倒するかどうかシミュレーションで確認してみようか」
草太「うん。転倒しないのは分かっているけど、どきどきするねぇ」
銀二「やっぱり転倒しないな。錘を付けてシミュレーションしてみよう」
台車の錘の重さをパラメータとして、台車が転倒するために必要な重さをシミュレーションで求めてみました。
図4.7に、錘の質量と転倒角度の関係をシミュレーションから求めた結果を示します。
草太「シミュレーションから判断すると10.5g以下では転倒しないから 11gぐらいがちょうどいいみたいだ。僕の計算だと15gぐらいがいいってことだったから、手計算の結果とそれほど大きく違わないね。いずれにしてもこの程度の重量だったらM5のボルトとナットの組み合わせでいけそうだな」
銀二「じゃあ、実際にやってみようか」
シミュレーションのビデオと実験ビデオを比較してみましょう。
きちんと転倒しています。
草太「おう! うまくいった!」
参考までに、錘を構成するボルト・ナットのうちの1つのナットを外して錘の重さを9.5gとしたときのシミュレーションのビデオと実験ビデオも紹介しておきます。
銀二「ここまでくれば、もうできたも同然だ。今日は祝杯でも挙げようか」
草太「明日は休日だし、今日は泊っていくんだね」
銀二「モチのロンさ……」
草太「昭和の香りがする死語でんな」
次回は、台車の中のボールがシーソーの上に落ち、反対側のボールをバスケットの中に入れるというサブ・システム5の設計です。請うご期待! (次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 義手とロボットの手を共通化するPSYONICのバイオニックハンド「Ability Hand」
- 同じ機械なのに1号機はOK、2号機はNG 設計者を悩ませる“再現しない不具合”
- 高精度3Dスキャナー3機種を発売、自動検査や医療分野を支援
- 約3.5kgの力で打ち抜ける手動式卓上パンチプレス
- 新型コロナで深刻なマスク不足を3Dプリンタで解消、イグアスが3Dマスクを開発
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 製造業の情報を一元管理するDXプラットフォームの体験型施設を開設
- 令和版の健康サンダル? 否、感覚を増幅する「Nike Mind」が気になる件
- 幾何公差の基準「データム」を理解しよう
- 強度設計の出発点 “計算”より先に考えるべきこととは?
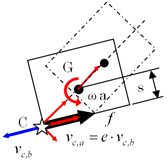 図4.5 衝突点の速度変化
図4.5 衝突点の速度変化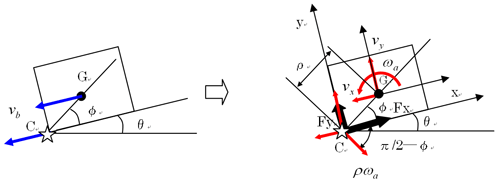 図4.6 台車がストッパと衝突するときの重心速度の変化
図4.6 台車がストッパと衝突するときの重心速度の変化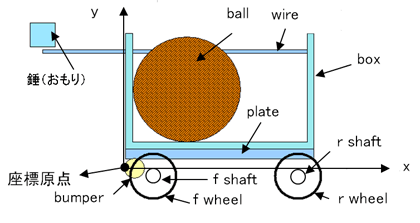 図4.7 台車に錘を付ける
図4.7 台車に錘を付ける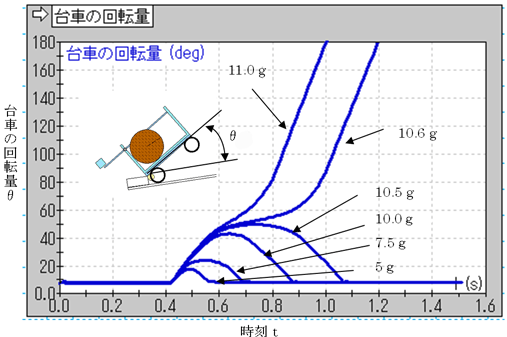 図4.7 ストッパ衝突時の台車の回転角度θと錘重量の関係(ストッパ衝突時の台車の回転軌跡)
図4.7 ストッパ衝突時の台車の回転角度θと錘重量の関係(ストッパ衝突時の台車の回転軌跡)






