“マイコンの出現”が本格カーエレ時代の幕を開けた!!：知っておきたいカーエレクトロニクス基礎（4）（1/3 ページ）

自動車用電子制御回路の基本と、それを構成する素子や回路について解説。これを理解すればカーエレを深く知ることができる。

[河合寿（元 デンソー） （株）ワールドテック，＠IT MONOist]

　連載第3回「エレクトロニクスを制する者は、カーエレを制す」では、“カーエレクトロニクスに関する電子制御回路の基礎”をテーマにお届けしました。

　今回も引き続き同じテーマで、

• オペアンプ（Operational Amplifier）
• 論理（ロジック）回路
• 電界効果トランジスタ（FET：Field Effect Transistor）
• マイクロコンピュータ（マイコン）
• 電子制御ユニット（ECU：Electronic Control Unit）

について解説していきます。

　前回と同様に少し堅苦しい内容ではありますが、ここをきちんと理解することが“カーエレクトロニクスを理解することの近道”だと思ってぜひ最後までお付き合いください。

オペアンプの構成および特長・事例

　オペアンプは、多くの「Tr（トランジスタ）」を使用した理想的な増幅器のアナログICです。図1にオペアンプの内部回路の概略を示します。

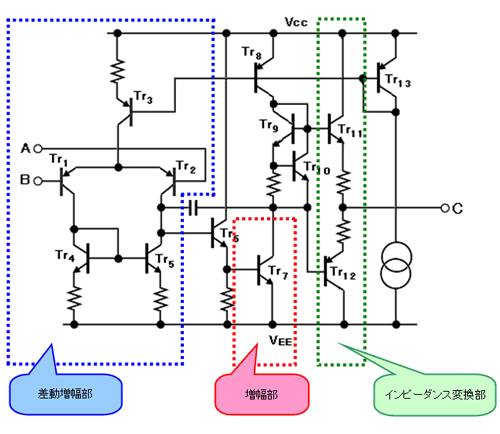図1　オペアンプの内部回路

　入力の差動増幅部は入力インピーダンスを大きくし、2つのTrの入力電圧の差を増幅します。差動にすることで、2つの入力信号に共通する温度やノイズによる影響を相殺します。次のエミッタ接地の増幅部でさらに増幅します。そして、NPNとPNPの2つのTrをエミッタフォロワ回路のインピーダンス変換部にして、インピーダンスを下げて出力します。

　以上の構成により、オペアンプは次のような特性を持ちます。

1. 入力インピーダンスが数100kΩ以上
   
2. 出力インピーダンスが100Ω以下
   
3. 開ループ利得（負帰還を掛けないときの利得）が1万以上
   
4. 帯域幅が広い
   
5. 内部ノイズが小さい

　次に、オペアンプの使用例を示します（図2）。

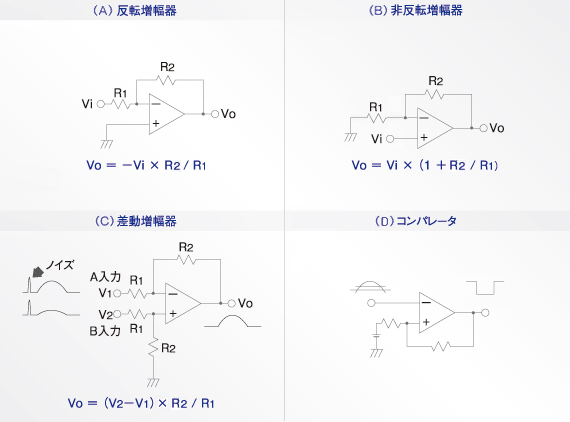図2　オペアンプの使用例

　図2（A）は「反転増幅器」です。増幅度は「R2 ／ R1」、つまり抵抗の比で決まります。Trで増幅回路を組んでいたころには考えられないくらい便利なもので、出力電圧は入力電圧の反対の極性になります。

　図2（B）は「非反転増幅器」です。増幅度は「（ 1 ＋ R2 ／ R1 ）」です。出力電圧は入力電圧と同じ極性が得られます。なお、反転増幅器も非反転増幅器も増幅度100（40dB）以上では理論どおりに動作しません。

　図2（C）は「差動増幅器」です。この差動増幅器はTrで組むには難しい回路でした。それがオペアンプを使用することでいとも簡単に実現できるようになりました。差動増幅器の特長として挙げられる機能に「同相成分除去（CMR）」があります。図2（C）の波形はその様子を示します。入力ラインに乗るノイズはA入力にもB入力にも同じ時期に、同じ大きさで同相で入ってきます。差動増幅器ですから、この同相成分のノイズを相殺できます。この相殺能力を「同相成分除去比（CMRR）」といいます。この値は周波数にもよりますが、オペアンプ1kHzで約60dB（1000倍）以上あります。例えば、CMRRが60dBとしますと同相ノイズの影響を1000分の1に低減できます。これはオペアンプだからこそできる芸当です。同様に電源電圧の「変動除去（PSR：パワーサプライリジェクト）」も可能です。

　図2（D）は「コンパレータ（比較器）」です。入力電圧「Va ＞ Vr」時に出力は“H（High）”から“L（Low）”になります。このほか発振回路やフィルタ回路などいろいろな回路にも使用されています。また、低ノイズ用や高周波用などの特長を持ったオペアンプも存在します。

関連リンク：
	【問題19】 オペアンプによる増幅回路（1） http://monoist.atmarkit.co.jp/fembedded/eledrill/1term/21.html
	【問題20】 オペアンプによる増幅回路（2） http://monoist.atmarkit.co.jp/fembedded/eledrill/1term/22.html
	1学期の集大成！ 【期末考査】のお知らせ http://monoist.atmarkit.co.jp/fembedded/eledrill/1term/23.html

デジタル回路における論理回路、組み合わせ回路や順序回路

　デジタル回路は、H（または“1”）レベルとL（または“0”）レベルの2つのレベルしか持たないため、数を扱うには2進数が便利です。われわれの生活では10進数を使っていますが、デジタル回路ではこれを2進数に変換して用います。

　この2値論理の変数を“論理変数”といい、この論理変数による演算を“論理演算”といいます。どのような論理演算も基本論理演算「AND（論理積）」「OR（論理和）」「NOT（否定）」の組み合わせで実現できます。図3に基本論理ゲートと論理記号を示します。

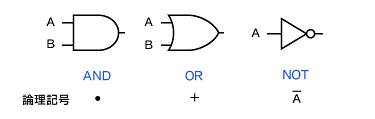図3　基本論理ゲートと論理記号

　図3のAとBは論理変数です。論理変数と論理記号により表される関数を“論理関数”といいます。例えば、

f（ A , B ） ＝ A ＋ B　……式1

などです。そして、論理式や論理関数を実現する回路を“論理回路”といいます。式1の論理回路を図4（A）に示します。

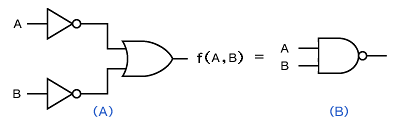図4　式1の論理回路

　さらに、式1は“ド・モルガンの定理”により「 A ＋ B ＝ A ・ B 」となり、論理回路は図4（B）のような簡単な回路になります。複雑な論理関数も定理や法則を使って簡単な論理関数にしてから論理回路を組んだ方が回路規模を小さくできます。

　“組み合わせ回路”とは、出力がその時点の入力の値によって決まる論理回路です。入力と回路の内部情報の両方から決まる論理回路を“順序回路”といいます。これは、いまの状態を記憶してその状態に応じて次の出力を決めていく回路ですから、記憶回路や組み合わせ回路でできています。最も基本的な記憶回路は「RSフリップフロップ回路（RS-FF）」です。図5（A）に論理回路を、図5（B）に真理値表（論理関数の取り得るすべての値を表にまとめたもの）を、図5（C）にタイムチャートを示します。

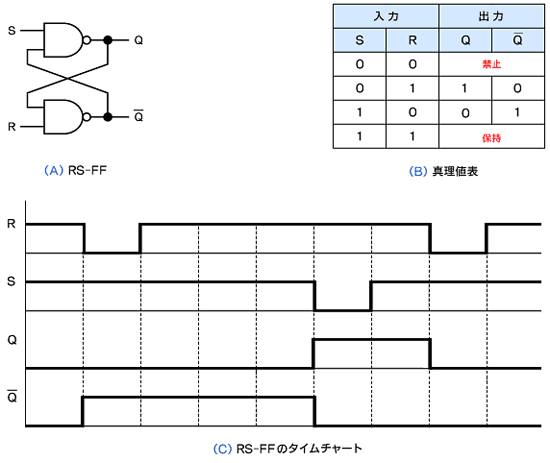図5　RSフリップフロップ回路

　図5（A）を見てください。襷（たすき）掛けしているところが“ミソ”です。タイムチャートから、Q出力においてR入力にパルス（ここではLパルス）が入ってからS入力にパルス（ここではLパルス）が入ってくるまでは“L”、S入力にパルスが入ってからR入力にパルスが入ってくるまでは“H”に保持（記憶）されます。

　このRS-FFを基本に組み合わせ回路を接続することで、さまざまなフリップフロップが実現できます。図6（A）は「D（Delay）-FF」、図6（B）は「JK-FF」、図6（C）は「T（トリガ）-FF」です。

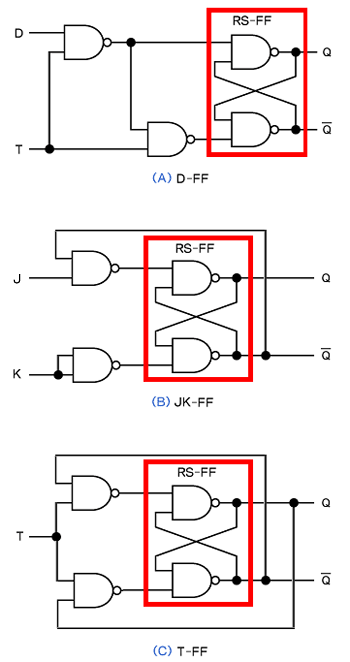図6　代表的なフリップフロップ

　これらフリップフロップは、それぞれ特長を持っており、複数接続することでメモリやカウンタ、レジスタなどを実現できるものもあります。これらの論理回路はファンクションごとにまとめられてIC化されています。

　論理ICの代名詞といえばバイポーラ（Bipolar）のTTL（Transistor-Transistor Logic）の74シリーズが有名ですが、現在では低電力化を実現した74LS（低電力ショットキーTTL）シリーズが使用されています。また、「CMOS（Complementary Metal Oxide Semiconductor）」といえば当初は4000シリーズでしたが、現在では74HCシリーズが使用されています。例えば、○○74LS00とは2入力NANDゲート×4のIC、○○74HC00はCMOSの2入力NANDゲート×4のICを指します。

関連リンク：
	連載記事「完全マスター！ 電子回路ドリル II」 http://monoist.atmarkit.co.jp/fembedded/index/eledrill2.html