設計で欠かせない「ミーゼス応力」を押さえよう:仕事にちゃんと役立つ材料力学(4)(3/3 ページ)
せん断について
ここで、「せん断」という言葉について理解しておきましょう。
「せん断力」とは、モノの内部で擦れ違うように働く力のことです。ある物質内の任意の平行面に関して、それぞれの面に反対方向に力を作用させた場合に発生します。具体的には、四角いものを平行四辺形に変形させる力の掛け方です。ハサミはこのせん断力によって紙を切断しています(図5)。
せん断力について、うまい説明が以下のサイトに出ています。アニメーションもありますので、ぜひご覧ください。
さて、先ほど登場した部品を応力解析してみました(図6)。
この応力のアニメーションを見ると、いろいろなことが分かります。
- 応力は、部品の形や荷重の大きさ、位置、方向によってさまざまな分布を示します。
- 応力は、一様ではなく、小さいものや大きいものがあります。アニメーションでは、黄色くなる部分は大きな応力で、青い部分はほとんど応力が発生していないことを意味します。
- 応力は、材料を引っ張る方向でも、圧縮する方向でも発生します。
そして、応力が材料の持つある値を超えると、その材料には強度を期待できなくなってしまいます。応力がある値以上にならないよう設計するために、事前に応力を知ることは、設計に大変有意義なことなのです。
Von Mises応力とは
これまでに、応力には垂直応力やせん断応力などの成分があるということを確認してきましたが、設計にはどんな応力(成分)を使えばいいのでしょうか? そもそも前に示したアニメーションはどんな種類の応力なのでしょうか? 垂直応力? それともせん断応力? 実は、どちらでもありません。
ここで、実際の設計者解析ツールにある機能を見ていきます。
「CATIA V5」(ダッソー・システムズ)には、作成した部品をカンタンに解析できるモジュールがあります。まず1つは、そのモジュールの解析結果の表示コマンドです。
そしてもう1つは、「SolidWorks」(ソリッドワークス)の解析モジュールである「COSMOSWorks」です。SolidWorksのモデルとシームレスにつながった設計者のための解析環境を提供しています(図7)。
CATIA V5の方は「Von Mises応力」が結果表示アイコンとして常備されています。一方、COSMOSWorksの方も結果表示の標準値としてVon Mises応力がすでに選択されています。それは垂直応力でもせん断応力でもないのです。
とうとう、ここまでたどり着きましたね!
設計にとって非常に大切な応力、それがVon Mises応力なのです。その証拠に、CATIA V5やCOSMOSWorksの例をはじめとして、設計者CAEツールのほとんどのソフトがこの応力をワンタッチで表示できるようになっています。
読み方、書き方はいろいろで、「ミーゼス応力」「ミゼス応力」、日本語で「相当応力」といったりします。垂直応力やせん断応力は忘れてもいいですから、この「ミーゼス応力」という言葉だけは、どうか忘れないでください。
「Von Mises」というのは人の名前です。リヒャルト・フォン・ミーゼス(Richard von Mises)氏は20世紀初めに活躍した科学者です。応力は、垂直応力3成分、せん断応力3成分で合わせて6つの成分がありますが、ミーゼス氏は「ある式で6つの成分を統合すれば、プラスもマイナスもない、1つの値で応力を表現できる」ということを発見しました。これは、ミーゼス氏の大きな功績といえます。
ミーゼス氏の理論を用いれば、材料の持つ固有の値で比較することによって強度を判定できるのです。材料力学という学問が現場で役立つ知識として交錯する瞬間です。
ミーゼスの式がどんなものか? この連載では「数式を使わない」というお約束ですので省略します。興味のある方は調べてみてください。大変美しい式です。
主応力の素顔
もう1つ、設計にとって非常に大切な応力、それが「主応力」です。主応力をきちんと説明しようとすると、やれ「座標系」だの、やれ「座標系の回転」だの、いろいろとややこしい話をしなければなりません。そのような解説は書籍の参考書に譲り、ここでは“主応力の素顔”を説明します。
ミーゼス応力は大きさのみを持つスカラー値でしたが、主応力は大きさと方向を持つベクトル値です。ミーゼス応力だと応力の方向は分かりませんが、主応力なら応力の方向が分かるということになります。つまり、部品にダメージを与えようとしている応力の大きさと方向が分かるのです。応力の方向と直角に切り欠きがあれば、部品の破壊はそこから始まるというわけです。
一般的な設計者解析ツールの結果表示には、ミーゼス応力と並んで主応力の表示アイコンも常備されています。結果表示ではもちろん垂直応力、せん断応力それぞれ3成分も表示できるようになっていますし、解析誤差がどれくらいあるかを表示したりもできます。
ミーゼス応力と最大主応力が設計にとって非常に大切な応力であるということをくれぐれも忘れないでくださいね。
。oO 筆者のつぶやき
ベクトルとスカラー
「スカラー」や「ベクトル」などの言葉が出てきましたが、これはとても身近な物理量なんです。天気予報には、ここで解説したスカラーやべクトルが具体的に登場します。「関東地方の天気は晴れ。気温12度」。この気温がスカラーです。温度には「大きさ」はありますが、「方向」はありません。 「北北東の風、8メートル」、この風はベクトルです。風には風速という「大きさ」と「風向き」という「方向」があります。つまり、「大きさ」と「方向」を持つからベクトルなんです。
応力は、テンソルである
材料力学の教科書には「応力はテンソルである」というくだりが出てきます。「テンソル? 何それ?」と、いろいろ調べてみて分かったことは、スカラーは「0(ゼロ)階のテンソル」で、ベクトルは「1階のテンソル」そして応力は「2階のテンソル」なんだそうです。……ますます分からなくなりました(笑)。物理学や数学が得意な人はこの説明だけで、応力をザックリと理解してしまうそうです。何ともまあ、うらやましい限りですよ。
◇
今回で応力の説明は終わりです。皆さんのアタマの中に応力というものがイメージできたでしょうか? さて次回はもう1つの大切な概念である「ひずみ」について解説を進めていきたいと思います。 (次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
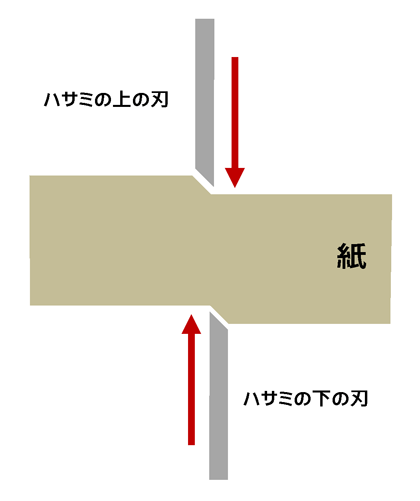 図5 ハサミが紙を切断する原理
図5 ハサミが紙を切断する原理  図6 応力コンター図 アニメーション
図6 応力コンター図 アニメーション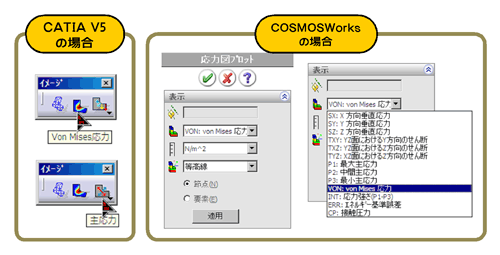 図7 CATIA V5とCOSMOSWorksのUI
図7 CATIA V5とCOSMOSWorksのUI 






