ど根性！ 1つ1つの寸法の係数を計算しよう：公差解析 実践の基本（2）（2/4 ページ）

今回はちょっと時間をかけて公差を計算してみた。疑いの目を忘れずに、くじけずに挑戦しよう。途中で居眠りしたら駄目っ！

[岡田あづみ／サイバネットシステム，MONOist]

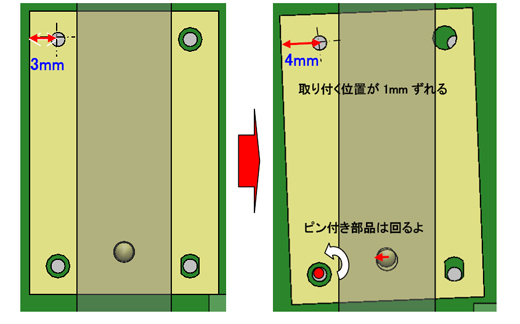
じゃあピン付き部品の寸法から見ていこうか。まず、穴の位置（No.1）がX方向に1mmずれるとどうなるかな……。

穴と長穴で位置を決めるから、部品自体は傾くわね。バカ穴を中心に部品が回転しているのかしら。

図3 取り付けるとピン付き部品は傾く

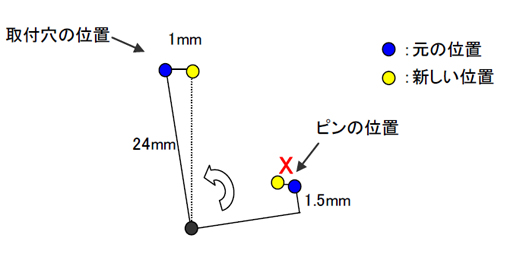
ピンと穴の位置関係も変わるねぇ。その量を計算すればいいのか！ 点と線で簡単に関係を書いてみよう。バカ穴からの寸法も幾つか入れてみたよ。

図4 ピン付き部品の寸法の変動と、知りたい箇所（Xの距離）

ありがとう、アズー。ここまできたら後は比で求まるわね。

　　　　　　　　24：1.5＝1：X

　　　　　　　　X＝1.5／24

　　　　　　　　　＝0.0625

この寸法（No.1）の係数は0.0625っと……。

この考え方はこのピン付き部品を組立てるボードの穴の位置（No.7）も同じだね。ボード側の穴の位置がばらついたら、ピン付き部品は同じように傾いて取り付けるしかないもんね。

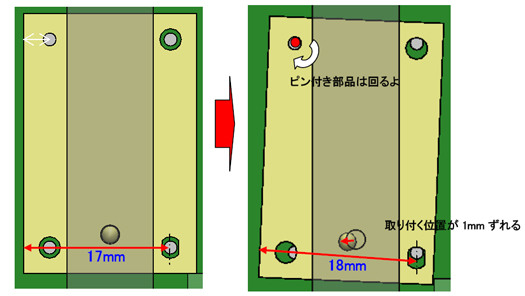
よし、次は同じピン付き部品の長穴の位置度（No.2）ね。

図5 取り付けるとピン付き部品は傾く

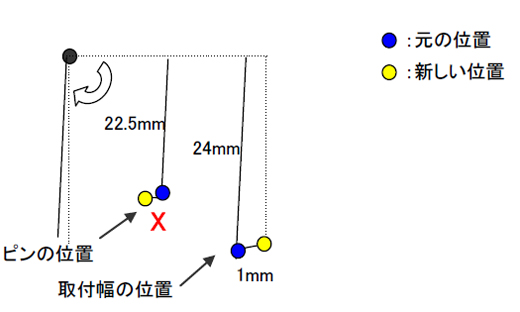
これまた傾いて取り付いちゃうね。今度は取り付ける穴を中心に傾くんだね。さっきみたいに点と線で書いて整理してみるか。

図6 ピン付き部品の寸法の変動と、知りたい箇所 その2（Xの距離）

関係を整理するのも、頭がこんがらがっちゃうな。……で、比を使ってこれも求めよう。

　　　　　　　　24：22.5＝1：X

　　　　　　　　X＝22.5／24

　　　　　　　　　＝0.9375

この寸法（No.2）の係数は0.9375ね。これも同じように、ボード側のこの長穴と締結される穴の位置（No.8）も同じ考え方で計算できるわね。