ど根性! 1つ1つの寸法の係数を計算しよう:公差解析 実践の基本(2)(3/4 ページ)
今回はちょっと時間をかけて公差を計算してみた。疑いの目を忘れずに、くじけずに挑戦しよう。途中で居眠りしたら駄目っ!
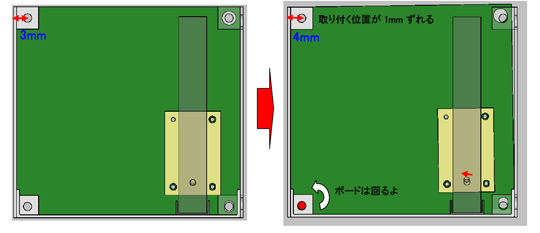
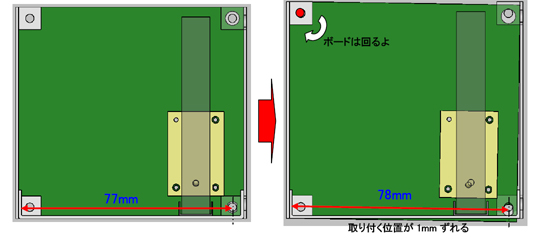
よし、じゃあ次はボードだね。No.5の取り付け穴の位置が1mm変動するとどうなる?
これもバカ穴を中心に傾くわね。関係はNo.1の時と同じ考え方ね。
よーし、じゃあNo.5の係数はこうなるね。
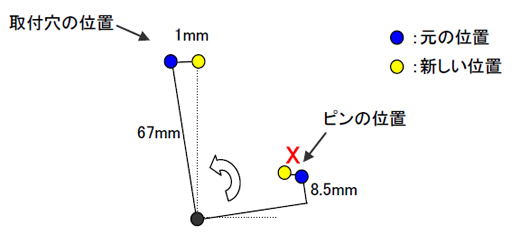
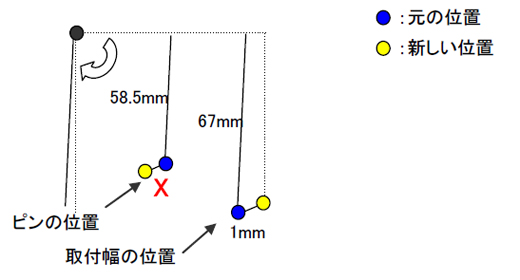
67:8.5=1:X
X=8.5/67
=0.12687
ねーねー、もう飽きてきたよー。
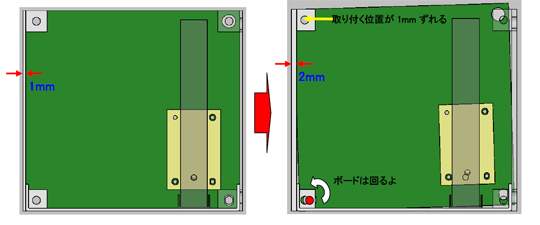
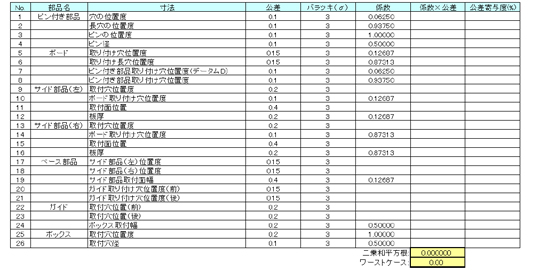
まだまだよ! 頑張るわよっ!! No.5の考え方はまだまだ応用できるわ。No.5の穴を取り付ける左側のサイド部品の穴の位置(No.10)も同じよね。
それから……実は、左側のサイド部品の板厚(No.16)もなんだよ。気付いたかな、君たち……ふっ。
おぉぉ! ホントだ!
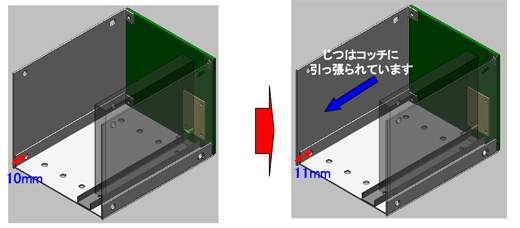
- 板厚が1mm増えるとベースに取り付く位置が1mmスライドする
- そして取り付け穴の位置も同じく1mmスライドする
っていうことダネ!
っつーことは、この板厚の件と同じことが、ベース部品のサイド部品を受ける面に入っている寸法(No.19)にも同じことがいえるんじゃない?
そう、その通り(図9-2)。……ふっ。気付いた俺すげー。
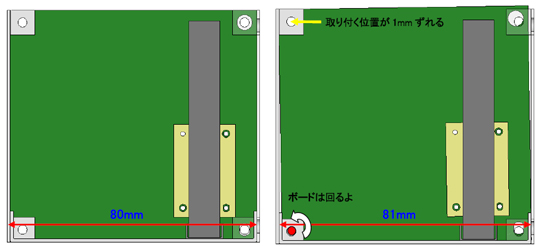
はいはい、じゃあ次いきましょ。No.6のボードの取り付け長穴の位置ね。
これはあれだね。“また傾く系”だね。
そうね。関係はNo.2の応用になるわね。回転中心からの距離で比を取って計算しましょ。
はーい。えっと……。
67:58.5=1:X
X=58.5/67
=0.87313
だから、No.6の係数は0.87313だね。そしてこの長穴と一緒に締結される右側のサイド部品の取り付け穴の位置(No.14)も同じ挙動……っと。さらにさらに! 右側のサイド部品の板厚(No.16)も取り付く位置のずれに直結するから、同じだね。
ムニャムニャ……。
さっきからホノさん静かだと思ったら、寝てるのか。
ちょっと髪の毛を整えてあげよう……ナデナデ。
うーん、……ママン。
びくっ! ホノさん!?
おぉ、どうやら少し目を閉じてしまっていたようだね。子どものころ、ママンに頭をいい子いい子、ってしてもらう夢を見ておったよ。お、もう結構進んだのう。済まない済まない。
あの、「ママン」……って。いや、これ以上突っ込むのはやめましょ。そうよ、ホノさん。もうここまで進んだのよ!
おぉ、ありがたいねぇ。じゃあどんどん進んじゃおう。次は左側のサイド部品の取り付け穴の位置(No.9)だな。
Copyright © ITmedia, Inc. All Rights Reserved.