ど根性! 1つ1つの寸法の係数を計算しよう:公差解析 実践の基本(2)(4/4 ページ)
今回はちょっと時間をかけて公差を計算してみた。疑いの目を忘れずに、くじけずに挑戦しよう。途中で居眠りしたら駄目っ!
うーん、よく分からない……。
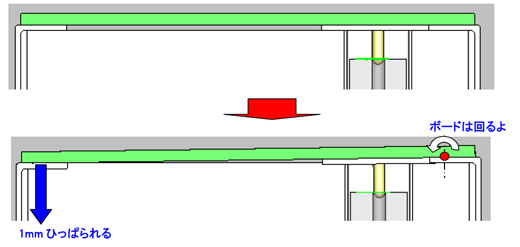
視点を変えた方がよさそうね。上から見るとこうなるわよ。左側のサイド部品がボードごと引っ張っちゃうのね。
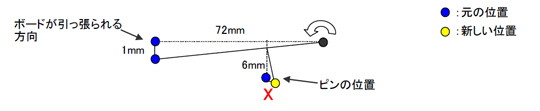
む、これはちょっとこれまでとはまた違うね。関係をまとめましょ! 回転中心になるのはボードと左側のサイド部品を締結する穴になるね。その引っ張られるポイントとの間で距離を取ると72mmになる。
寸法が動く方向と、評価したい方向が明らかに違うわね。この場合は頑張って計算するしかなさそうね。
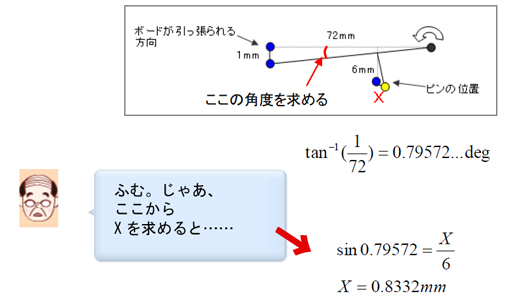
おーし、頑張ろうっ。まず傾く角度を計算しちゃおう。
おー、(No.9)の係数が求まったね。ということは、この穴と一緒に締結されるベース部品の方の穴(No.17)も同じ係数になるね。あと、同じ挙動はNo.11のボードが取り付く面の位置でも起こると思うな。
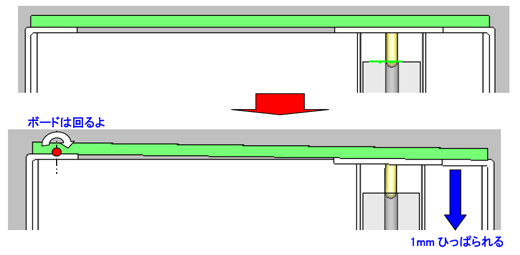
ボードの位置が引っ張られるのは同じだな。後は、右側の取り付け穴の位置(No.13)と面の位置(No.15)は挙動が正反対になるだけじゃないかな? ……ほら。
ホホ。回転角度が同じだから、ピンの先端の動き方も方向が逆になるだけだね。No.13とNo.15の係数も0.8332っと。えっと、No.13の穴と一緒に締結される、ベース部品の穴の位置(No.18)もだねー。
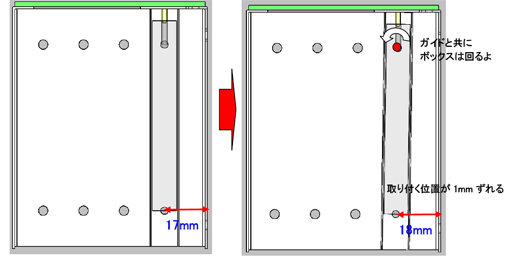
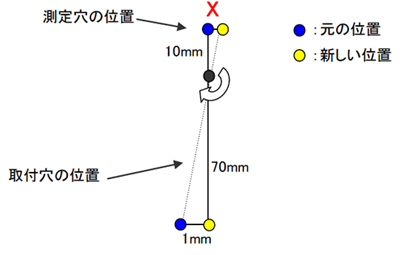
よーし、あと残り4つ! ベース部品のガイドを取り付ける穴の位置だね。ピンから遠い方の穴(No.20)から見てみよう。今度はボックス側の穴の位置が動いて、すき間に影響を与えるね。
よしきた。この関係は……。
じゃあ係数は……。
70:10=1:X
X=10/70
=0.14286
ガイド側でこの穴と一緒に締結される穴(No.22)も同じ係数になるね。
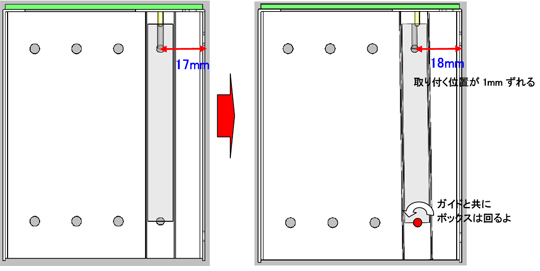
ではベース部品のもう一方の穴を見てみようか。挙動はさっきと似ているな、きっと。
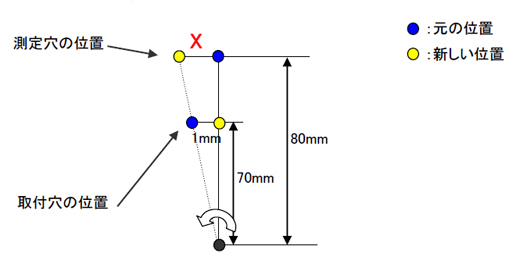
よー、じゃあこれはぺペイのペイで計算しちゃいますよ! 回転する基準になる穴と、ボックスの穴の先端までの距離は80mmだよ〜。
ではこれを計算してみると……。
70:80=1:X
X=80/70
=1.14286
No.21の係数は1.14286だね。あと、ガイド側でこの穴と一緒に締結される穴(No.23)の穴の位置も同じ係数になるのう。
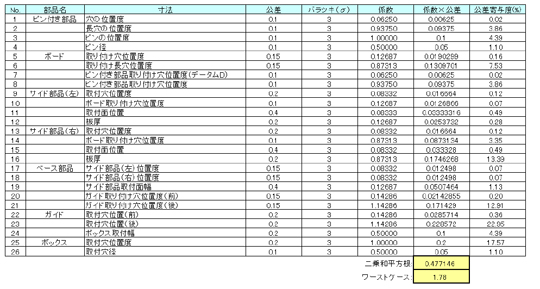
できたーっ! できたできたー! 係数が全部埋まったよ!!
むむ。この結果を見ると、よろしくなさそうだな。
思いっきりぶつかる確率は高いのかな……。
まだY方向の計算もあるわ。次回までにY方向の計算をして、まとめてちょっと考えましょ。
「キカコーサ……」「重力……」「ガタ……」「忘れないで……YO!」
――どこかから声が聞こえてきます。
どこからかおじさんの声が!? 気のせい?
さー、今日はここのところで帰るぞ!(肌色クローバーちゃん! 待ってて!)。
妙にナオってばイソイソしてるわね。でも疲れたから今日はここのところで帰りましょ。
ばーかにゃうだ♪ ばーかにゃうだ♪
才羽工業の製品での公差解析は、まだまだやることがありそうな感じですが、今日のところは、ひとまずここで一区切りです。
ここまでのおさらい
今回は時間をかけて1つ1つの寸法の係数を計算していきました。どうでしょうか。ちょっと面倒ですね。飽きっぽい私は何度もくじけそうになりながら計算をしました。
評価したい箇所に影響する寸法は3次元の空間の中にたくさんちりばめられています。これを洗い出していく中で、必要ない公差を足してしまうのも、逆に関係あるのに見落としてしまうのも人次第だったりします。慎重に「この寸法がばらついたら、組み立て精度に影響はないだろうか」という疑いの目を忘れずにピックアップしてください。
そして係数の計算。これも寸法がばらつくことで、「どんな風に部品が傾くのか?」「組み立て精度はどうなるのか?」、丁寧に分解してあげることで正しい係数は出てくるはずです。
しかし、まだまだこのお題には課題が残されています! これからもうしばらくお付き合いくださいね。(次回へ続く)
Copyright © ITmedia, Inc. All Rights Reserved.