コンデンサーを用いた実験回路で微分積分の本質に迫る【積分編】:今岡通博の俺流!組み込み用語解説(15)(2/2 ページ)
積分の実験回路
ここまで幾つか事例を挙げた積分を電子回路で確かめてみましょう。図1は積分の動作を確かめる実験回路です。
抵抗とコンデンサーが用いられており、電子回路としてはRC積分回路として知られています。Rは抵抗で18kΩです。Cはコンデンサーで47nFです。
積分回路の特徴は、入力(IN)と出力(OUT)の間に並列にコンデンサーが挟まれていることです。微分回路は入力と出力の間に直列にコンデンサーが挟まれていましたが、積分回路は抵抗とコンデンサーが入れ替わった回路になっていますね。
それでは、この積分の実験回路と2つの信号を同時に観測できる2現象オシロスコープを使って、入力側の波形と出力側の波形を比較することでコンデンサーによって引き起こされる積分現象を観測したいと思います。
さまざまな波形を使って積分現象を確かめる
今回の実験では、筆者が所持しているハンディーオシロスコープ「OWON HDS272S」を用いて観測します。このオシロにはシグナルジェネレーターの機能があり、これで生成した信号を入力信号とします。入力信号は1Vpp(波形の振幅の山から谷までの電位差が1V)で、周波数は1kHzです。
なお、各入力波形の説明は微分をテーマにした前回記事を参照してください。
正弦波
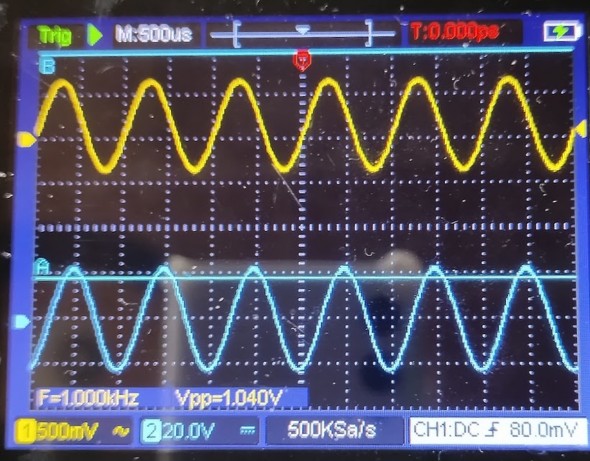
それではまずは正弦波の波形から見てみましょう。図2は正弦波の入力波形と出力波形を比較するためのものです。
図2内の2つの波形のうち、上側の黄色い波形が入力信号で、下側の水色の波形が積分回路の出力波形です(オシロの画面の撮影に使ったスマホが写りこんでいますが、気にしないでください)。このオシロ、スクリーンショットが取れればいいのですが、方法が分かりません。もしできるようであれば図2は後日差し替えたいと思います。
さて、この波形の解釈ですが、数学で学んだところによると正弦波(sin)を積分すると負の余弦波(−cos)になります。これは微分回路では90度波が進んだのに対して、積分回路では90度遅れるためです。
矩形波
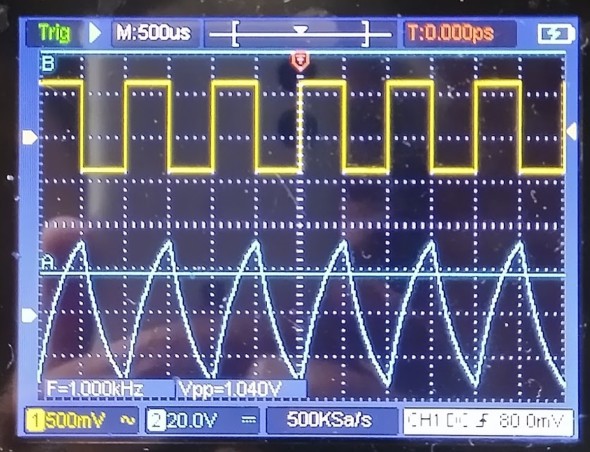
図3は矩形波の入力波形と、積分回路を通した後の出力波形を表示したものです。
この出力波形は、入力波形の矩形波の谷の部分でコンデンサーが放電し出力波形は下り坂となります。一方矩形波の山の部分ではコンデンサーは充電されますので徐々に電圧が上がっていきます。これを繰り返すことにより三角波のような波形になります。
ノコギリ波
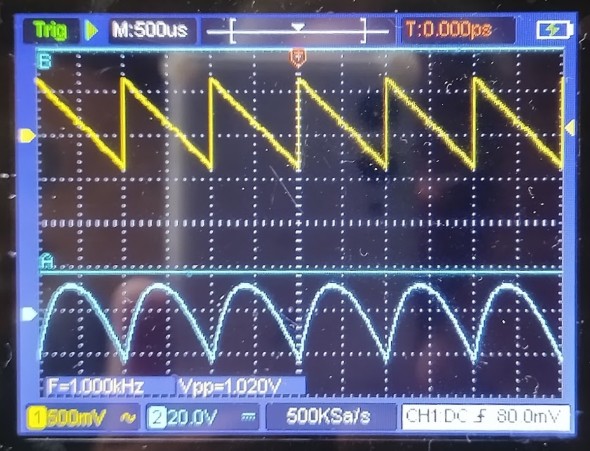
図4はノコギリ波の入力波形と、積分回路を通した後の出力波形を表示したものです。
入力波形のノコギリ波が急激に上昇する時点から充電が開始され多少時間差があるものの出力波形も上昇していきます。入力波形がピークを過ぎた下り坂局面ですが、この時点でもしばらく充電は継続し、入力電圧がある一定電圧を下回るとそこをピークに電圧が下がり始めます。ノコギリ波を積分すると図4のように半円を伏せたような波形になります。ノコギリ波の上昇地点に波形がやや傾くような波形になっていますね。
おわりに
いかがだったでしょうか。まあ感覚的でもよいので少しでも積分の理解が深まり、興味が沸いたでしょうか。よりきちんと微分積分を理解したい方は、数式が出てくる解説記事が多数ありますので、そちらでさらに理解を深めていただければと思います。
関連記事
- ≫連載「今岡通博の俺流!組み込み用語解説」バックナンバー
- ≫連載「注目デバイスで組み込み開発をアップグレード」バックナンバー
 コンデンサーを用いた実験回路で微分積分の本質に迫る【微分編】
コンデンサーを用いた実験回路で微分積分の本質に迫る【微分編】
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第14回は、数学が苦手になる原因の一つである微分積分のうち微分について、コンデンサーを用いた実験回路を使ってその本質に迫る。 「コイル」は受動素子ナンバーワンの不思議ちゃん
「コイル」は受動素子ナンバーワンの不思議ちゃん
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第13回は、受動素子ナンバーワンの不思議ちゃんである「コイル」を紹介する。 オペアンプをコンパレーターとして使って見る
オペアンプをコンパレーターとして使って見る
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第12回は、オペアンプをコンパレーターとして活用する事例を紹介する。 組み込み技術者のためのコンデンサー活用術
組み込み技術者のためのコンデンサー活用術
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第11回は、組み込み技術者やデジタル技術者が知っておくとよいであろうコンデンサーの活用術を紹介する。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- パナソニックの弱いロボット「NICOBO」がLLMでさらなる進化、累計販売は1万体に
- ソニーがSTB不要のデジタルサイネージを提案、AIデジタルヒューマンも組み込める
- Rapidusの顧客獲得が進捗、60社以上と協議中で約10社にPDKをライセンスへ
- あなたの家電がサイバー攻撃の踏み台に? 購入時は星マークをチェックしよう
- 家電のノジマがロボットショールームにヒューマノイドや業務用を展示する理由
- スバルが制御統合ECU向けマイコンにインフィニオンの「AURIX TC4x」を採用
- チップレットでASIL Dを支援する車載SoC技術を開発
- 製造業の「SBOM」は誰が構築し運用/管理すべきか【後編】
- 一度の顔登録で複数サービス利用可能 NECの顔認証基盤、トライアルなどで実証導入へ
- 出荷量1.3倍を実現、電源不要のIoTゲートウェイが南種子町にもたらす農業改革
コーナーリンク
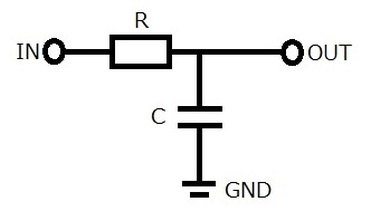 図1 積分の動作を確かめる実験回路
図1 積分の動作を確かめる実験回路