フローで考えるモデリング 〜さまざまな現象を統一的に扱う方法〜:1Dモデリングの勘所(28)(3/4 ページ)
現象をフローで考える:機械(振動)の場合
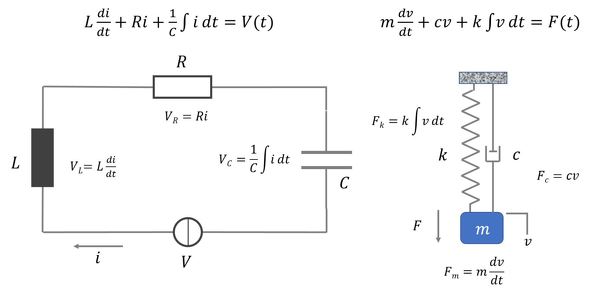
連載第4回で述べたように、機械(振動)に関する式は以下で定義できる。
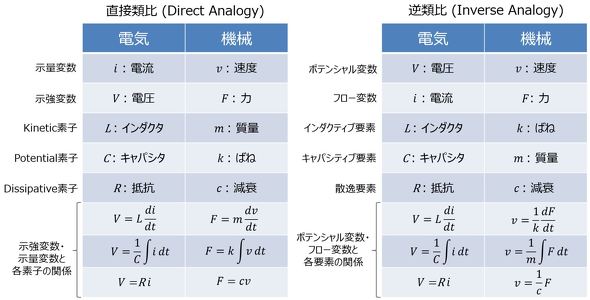
mは質量、cは減衰、kはばね、vは速度、Fは力である。今までの電気、流れ、熱の対比から考えると、速度がフロー変数となるが、実際には速度をフローと考えるのは難しい。これは、図4に示すように電気と機械は式としては対応していて(これを「直接類比」という)、同様の手順で解くことができるが、図で表現すると各状態量と要素が必ずしも対応していない。
図4の問題を解消する方法として、力をフロー変数とする考え方を導入する。これを「逆類比」と呼ぶ。表2に電気と機械の直接類比および逆類比の場合の比較を示す。直接類比では状態量、要素の呼び方がそもそも逆類比とは異なっている。すなわち、直接類比にはもともと、フローという状態量の概念が存在しない。
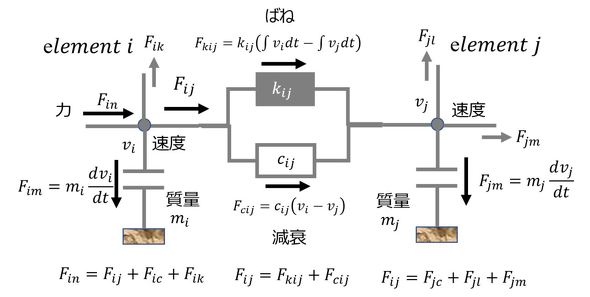
表2の逆類比に従って、力Fをフローとして考え、機械に関する現象のある部分をフローに即して図で表現すると、図5となる。
図5を式で表現すると、力の連続の条件(電流則)から、
となり、各要素の力(フロー)と速度(ポテンシャル)の関係(電圧則)から、
が成り立つ。このように、機械(振動)に関しても一工夫することにより、フローで考えるモデリングは可能となる。この方法は、連載第15回「モデリングツールとしての「Modelica」(その3)」で紹介した「Modelica標準ライブラリ(Modelica Standard Library)」の作成手順に対応する。
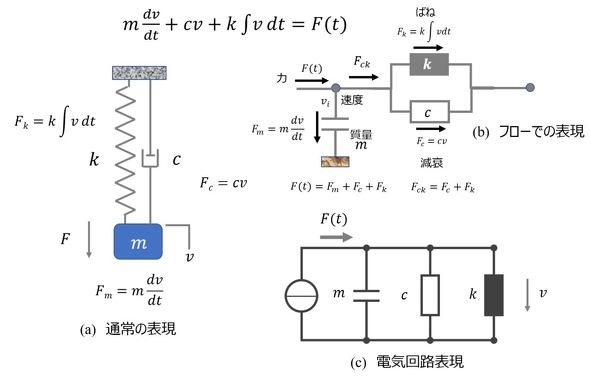
図6に一自由度系MCKモデルの通常の表現、フローでの表現、電気回路表現を示す。電気回路表現は、連載第12回「スピーカーのモデリング〜電気、機構、音響の連成問題、3つの現象を回路で表現〜」で説明したように、電気、機械、音響と連成した問題で威力を発揮するが、複雑な機械(振動)系の問題には適していない。通常の方法は、図表現が容易であるが、系が複雑になってくると力のつり合いを都度考える必要がある。これに対して、フローによる表現は複雑な系に対しても、半自動的に式を導出できる。いずれの方法も長所短所があるので、状況に応じて使い分ければよい。同じ機械(振動)問題であってもさまざまな表現や解法があることを知っていることが重要だ。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞