フローで考えるモデリング 〜さまざまな現象を統一的に扱う方法〜:1Dモデリングの勘所(28)(2/4 ページ)
» 2024年02月20日 09時00分 公開
[大富浩一/日本機械学会 設計研究会,MONOist]
現象をフローで考える:流れおよび熱の場合
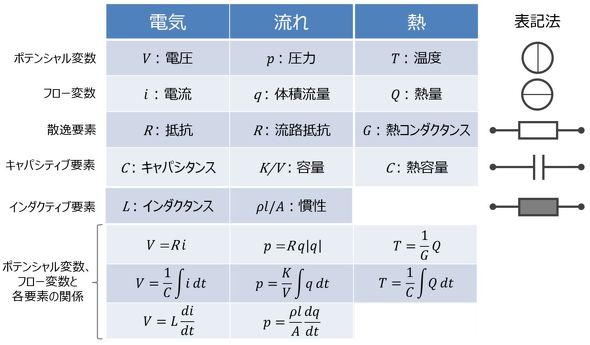
連載第5回でも述べたように、電気、流れ、熱に関する変数および要素に関しては、表1に示す関係が成り立つ。
つまり、流れおよび熱に関する現象に関しては、表1の対応に従って、電気の場合(図1)と同様の手順を踏み、フローに基づいて図で表現した後に、そこから式を定義すればよい。
流れの場合には、次式が成り立つ(この式の導出については以降の連載の中で説明する)。
ρ,l,Aは、流れ部分のそれぞれの密度、長さ、断面積、Rは流路抵抗、V,Kは容積部分の体積と体積弾性率、qは流量、pは圧力である。表1から、流れの場合は流量がフローであり、流れに関する現象のある部分をフローに即して図で表現すると、図2となる。
図2を式で表現すると、流量の連続の条件(電流則)から、
となり、各要素の流量(フロー)と圧力(ポテンシャル)の関係(電圧則)から、
が成り立つ。
同様に、熱の場合は次式が成り立つ。
Gは熱コンダクタンス、Cは熱容量、Qは熱量、Tは温度である。表1を見て分かるように、熱に関してインダクティブ要素は存在しない(あるいは、確認されていない)。表1から、熱の場合は熱量がフローであり、熱に関する現象のある部分をフローに即して図で表現すると、図3となる。
図3を式で表現すると、熱量の連続の条件(電流則)から、
となり、各要素の熱量(フロー)と温度(ポテンシャル)の関係(電圧則)から、
が成り立つ。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentsPR
Pickup ContentsPR
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現
Special SitePR
あなたにおすすめの記事PR
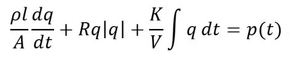 式8
式8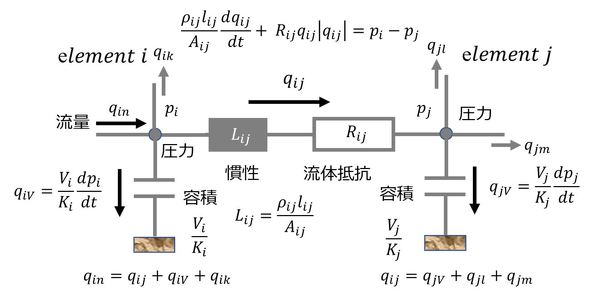
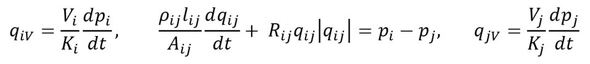 式10
式10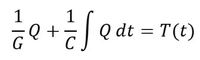 式11
式11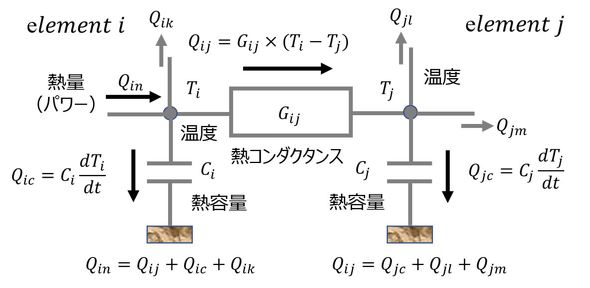
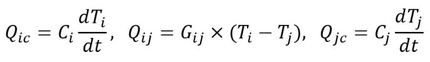 式13
式13





