【最終回】CAEと計測技術を使った振動・騒音対策の総まとめ:CAEと計測技術を使った振動・騒音対策(21)(1/3 ページ)
“解析専任者に連絡する前に設計者がやるべきこと”を主眼に置き、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。最終回となる今回は、これまでの内容を振り返りながら、連載の重要ポイントをおさらいする。
連載「CAEと計測技術を使った振動・騒音対策」もいよいよ最終回となります。今回はこれまでの内容を振り返りながら、連載の重要ポイントをおさらいしたいと思います。
横軸を周波数に変えて行動しよう
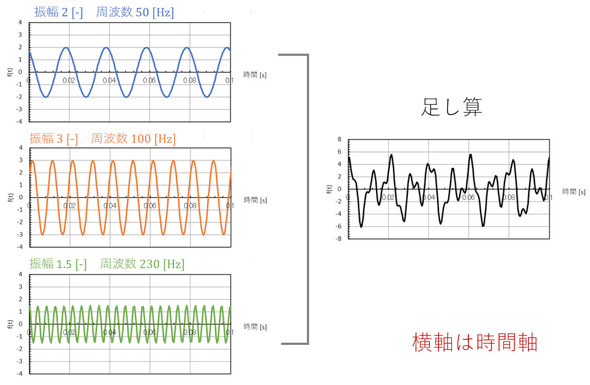
図1左図に、振幅2[-] 周波数50[Hz]のcos波、振幅3[-] 周波数100[Hz]のcos波、振幅1.5[-] 周波数230[Hz]のcos波を示します。図1右図はそれらの和です。
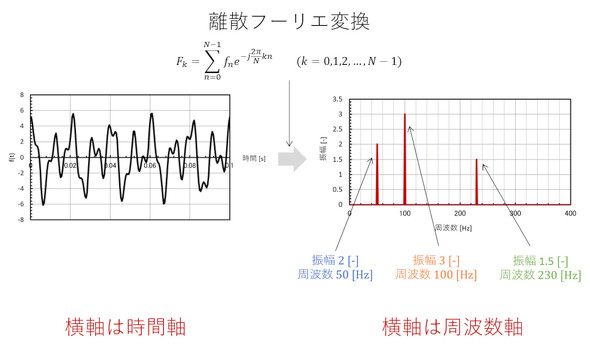
私たちが日常で行っている周波数分析はフーリエ変換ではなく離散フーリエ変換であること、FFTアナライザは「FDFTアナライザ」と呼ぶべきであることをくどいほど述べてきました。図2に3つのcos波の和を離散フーリエ変換したものを示します。図2右図の通り、周波数分析をすると元になったcos波の振幅と周波数が分かります。
また、フーリエ変換した結果をフーリエ逆変換すると、元の波形になるはずです。フーリエ逆変換と聞くと何だか難しそうな計算が必要な気がしますが、そんなことはなく、図1の計算が離散フーリエ逆変換に相当します。
図2左図のグラフの横軸は“時間軸”、図2右図の横軸は“周波数軸”であり、振動・騒音対策は横軸を周波数軸にして行動する必要があります。連載では、周波数分析をするためのマクロ付きExcelファイル(クリックでダウンロード)を公開し、高価なFFTアナライザを購入する必要がないことを紹介しました。
騒音・振動対策モデル
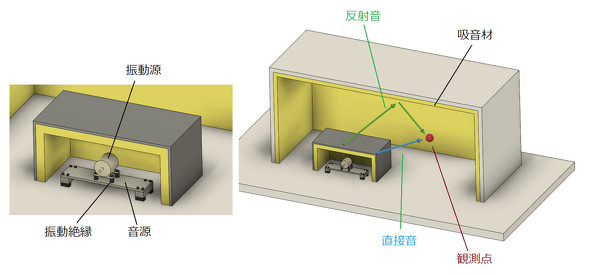
次に、図3のようなモデルを考えます。モーターのような振動源があるとします。板の上にモーターが載っかっています。モーターの表面積より板の方が面積が大きく、板から放射される音が支配的だったとします。この場合、板が音源になります。そして、音源を遮音壁で囲い、遮音壁の内側には吸音材を貼り付けておきます。続いて、人間がいる部屋を考えます。赤い球が人間の耳の位置で「観測点」と呼びます。部屋の壁にも吸音材を貼り付けておきます。このようなモデルの騒音対策を考えます。
全ての挙動を伝達関数で捉え、伝達関数を見て対策を立てていきます。伝達関数は次式でした。
伝達関数は「応答/入力」です。そして、応答は「伝達関数×入力」です。入力としては、エネルギーが考えられます。力であったり、最近の機械のほとんどは電気仕掛けなので電流だったりします。そして、その応答は振動速度などです。次の段階として、振動が伝わることを考えると、入力と応答は共に振動速度となります。さらに、板が音源だとすると、板の振動速度が入力で、放射される音圧が応答です。箱で遮音しているため、入力は箱の中の音圧、応答は箱の外の音圧です。このように全ての過程で伝達関数を定義できます。エネルギー源は入力になりますが、あらゆるステージの振動と音圧は入力にも応答にもなり得ます。ブロック図を図4に示します。
伝達関数は横軸を周波数として表現します。これは式1、式2にs=jωを代入することで求まります。ωは角振動数で単位は[rad/s]です。ω=2πfとなり、fは周波数です。伝達関数は次式となります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 設計者の思考を止めないという視点
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- AIに期待することは? 活用に向けた課題は? 設計/解析現場の本音を徹底調査

 式1、式2
式1、式2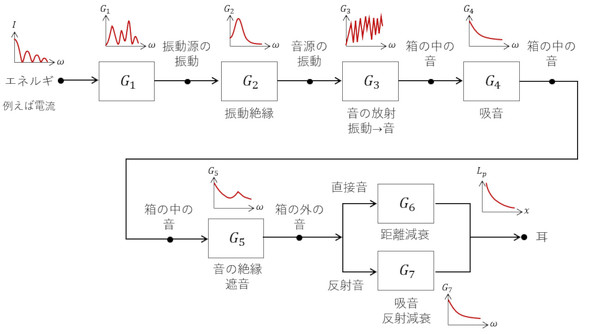
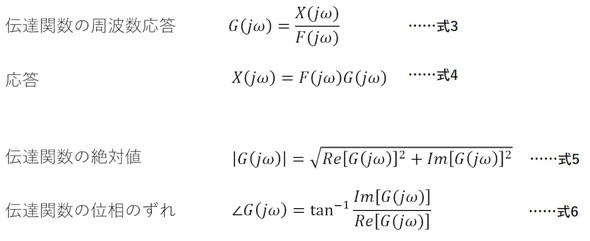 式3〜式6
式3〜式6





