【最終回】CAEと計測技術を使った振動・騒音対策の総まとめ:CAEと計測技術を使った振動・騒音対策(21)(2/3 ページ)
振動に関する伝達関数の例
図4の中にあるたくさんの伝達関数を見ていきます。全て連載の中で紹介したものになります。
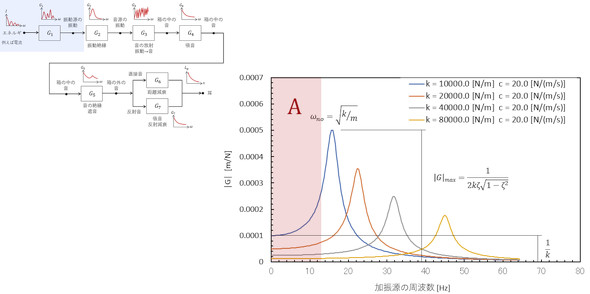
図4の伝達関数G1は、振動発生の伝達関数です。入力はエネルギーであり、力やモーターに流す電流値となります。応答は振動変位、速度、加速度になります。この伝達関数は、ばね−マス系を使って説明しました。
伝達関数G1の例を図5に示します。図5のA部に注目すると、ばね定数kを上げると振動変位が下がります。通常の機械の共振点は、ばね−マス系のように1点ではなく無数にあるので、伝達関数のピークの山と山の間に駆動源の周波数を持っていくと対策ができます。ただ、そのような器用なことができればいいのですが、筆者のように器用でない設計者はばね定数kを上げること、つまり装置の剛性を上げることばかりやってしまいがちです。
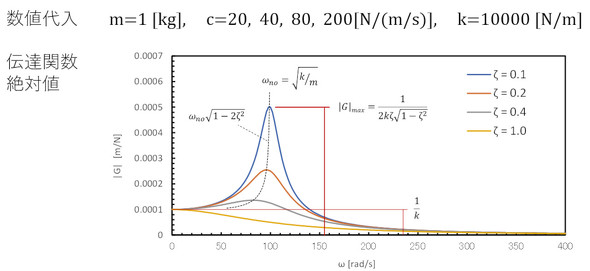
また、駆動源がインバーター駆動などで、力の周波数成分がたくさんあるときや連続スペクトルであるときは、抵抗に相当するもの(減衰物)を系に追加すべきです。そのときの伝達関数を図6に示します。抵抗に相当する量ζを大きくすると、共振点の伝達関数は見る見る下がります。しかし、共振点以外ではあまり効果が期待できないことにも注目してください。
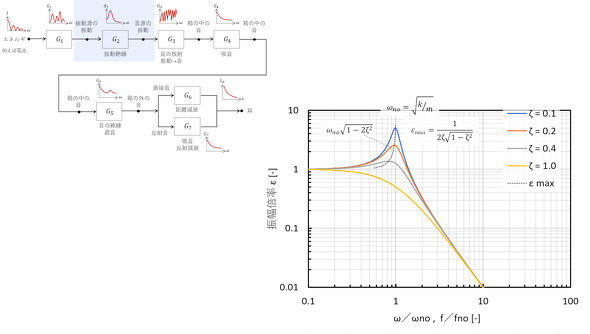
図4の伝達関数G2は、振動絶縁性能を表す量です。入力は振動変位、応答も振動変位の場合もあれば、入力は力、応答も力となる場合もあります。図7に振動絶縁に関する伝達関数を示します。「入力:振動変位 応答:振動変位」の場合と、「入力:力 応答:力」の場合で同じ形になります。共振点だと伝達される量は増加しますが、振動源の周波数が共振点よりも大きいと振動絶縁ができます。
騒音に関する伝達関数の例
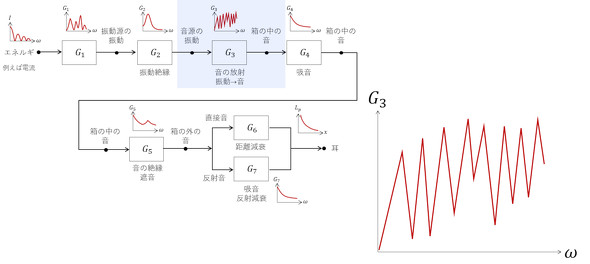
図4の伝達関数G3は、音の放射の伝達関数です。図8に音の放射に関する伝達関数を示します。入力は音源の振動速度、応答は音圧です。音源の振動速度と音圧が比例関係であることは、連載第2回で説明した通りです。振動を加速度ピックアップで測定することが多いと思いますが、その周波数分析結果を2πfで割って速度に変換する必要があります。伝達関数G3は無数のピーク周波数があり、図8のようにギザギザです。
図9は円柱状空間の音響モーダル解析結果です。固有振動数(共鳴周波数)は図のようにたくさんあります。人間が入れるようなサイズの空間であれば、可聴領域の中で共鳴周波数が無数にあります。今まで伝達関数を操作して対策を進めることを述べてきましたが、ここでは共鳴周波数は数十[Hz]〜無数にあるので、伝達関数の操作による騒音対策は絶望的になります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞