振動と音に関する基礎量 その2:CAEと計測技術を使った振動・騒音対策(3)(2/4 ページ)
音響インテンシティ
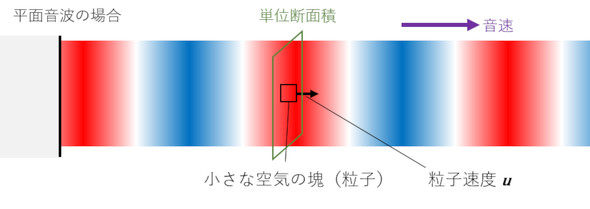
平面音波は図5に示すように圧力変動が音速で進行します。連載第2回で空気の小さな塊(粒子)が振動していることを説明しました。音響インテンシティの瞬時値は式3で定義されます(参考文献[1])。粒子速度はベクトル量なので、音響インテンシティはベクトル量となります。
瞬時音響インテンシティの時間平均が音響インテンシティです。これもベクトル量で次式となります。
音響インテンシティが意味するものを考えてみましょう。図6に音の伝搬方向に垂直な面Δsとその面の圧力pと粒子速度uを示します。
音波が垂直な面Δsを押す力fは次式となります。
時間Δtの間の面Δsの移動距離は次式となります。
Δt間に音波がΔsになす仕事は、力×移動量なので次式となります。
単位時間に面Δsに音波がなす仕事は次式となります。
単位時間に単位面積に音波がなす仕事は次式となります。
式9と式4を見比べると同じですね。というわけで、音響インテンシティは単位面積の面を通過する音のエネルギーです。
市販の音響インテンシティ測定器には、測定値をデシベル表示するものがあります。その定義を以下に記します。ちなみに、音響インテンシティは負の値を持つことがあるので、デシベル表示の使用について筆者は賛成していません。よって、ここではデシベル表示は使わないことにします。
球面音波について考えてみます。図7に出力W[W]の点音源から音が放射されている状態を示します。このような音源を「呼吸球」といいます。球の表面積は4πr2なので音源からの距離がr[m]のところの音響インテンシティの大きさは式11となり、音響インテンシティ方向は音源から遠ざかる方向となります。分かりやすいですね。
平面音波に戻ります。連載第2回で次式を紹介しました。平面音波なので粒子速度u(t)は一方向成分となりベクトル記号を外しています。
式12を変形します。
式13を式4に代入します。平面音波なのでベクトルを絶対値と表記します。この積分は連載第1回で述べた実効値を求める形なので、音響インテンシティの大きさは音圧の実効値の二乗をcρで割った値です。よって、音響インテンシティから音圧を求めることができます。
球面音波でも同じ式となります。
参考文献:
- [1]日本規格協会|音響−音響インテンシティによる騒音減の音響パワーレベルの測定方法|JIS Z 8736-1(2014)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 設計者の思考を止めないという視点
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
- 測量の常識を変えるハンディー型3Dスキャナー 歩くだけで空間を丸ごと3D点群化
- 直径2.5mの巨大アートを3Dプリント、カーボンリサイクル素材で実現

 式3
式3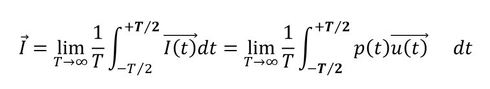 式4
式4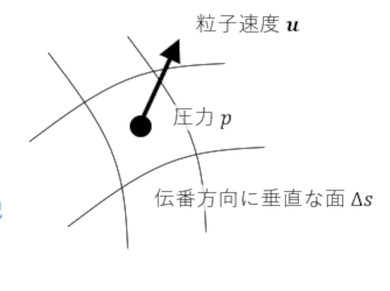
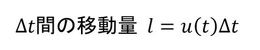 式6
式6 式8
式8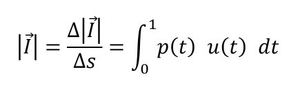 式9
式9 式10
式10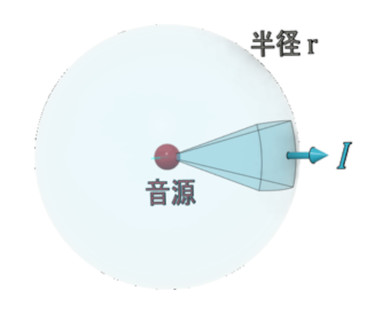
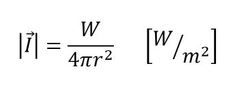 式11
式11 式12
式12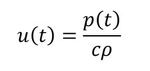 式13
式13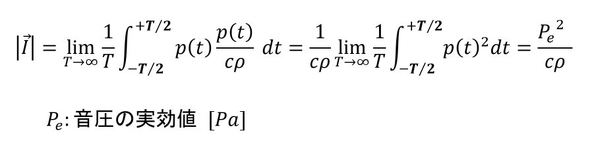 式14
式14





