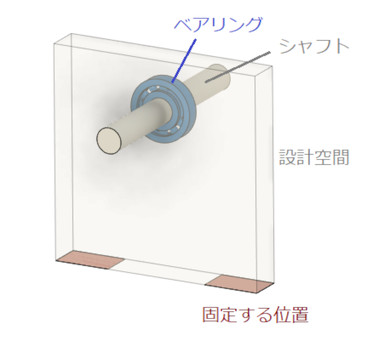
　今度は、ベアリングサポートの形を求めましょう。図18の位置にシャフトとベアリングがあり、赤色で示した面でベアリングサポートを固定するとしましょう。グレーの透明体は設計空間です。ベアリングの位置と固定する位置を指定して、ひずみエネルギーが最小になるようなベアリングサポートの形を決めてくださいという問題です。

図18　ベアリングサポートの設計空間［クリックで拡大］

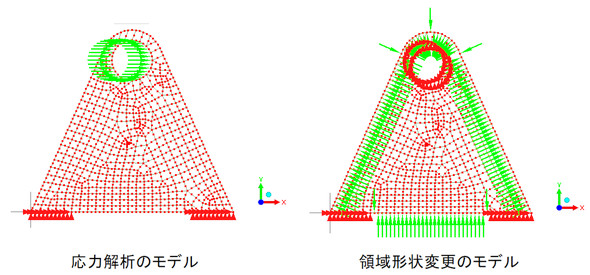
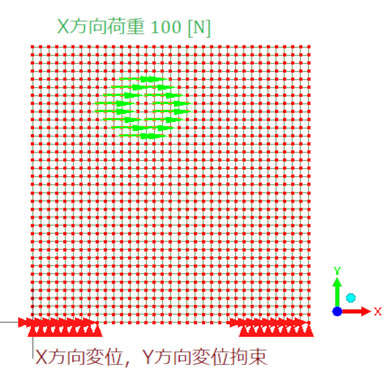
　応力解析のモデルと領域変更の解析のためのモデルの初期形状を図19に示します。

図19　ベアリングサポート領域最適化解析モデル［クリックで拡大］

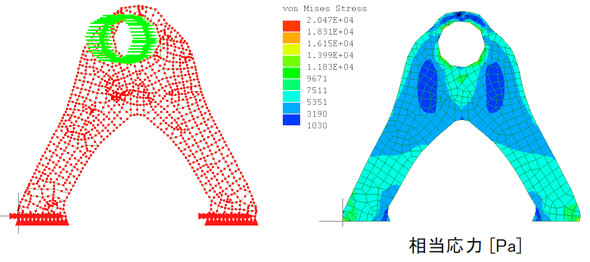
　領域最適化では節点座標が移動するため、要素がいびつな形となって解析ができなくなります。よって、途中で2度、リメッシュを行いました。最適化形状を図20に示します。ちょっと冴えない形になりましたが、これが解です。

図20　ベアリングサポート領域最適化結果［クリックで拡大］

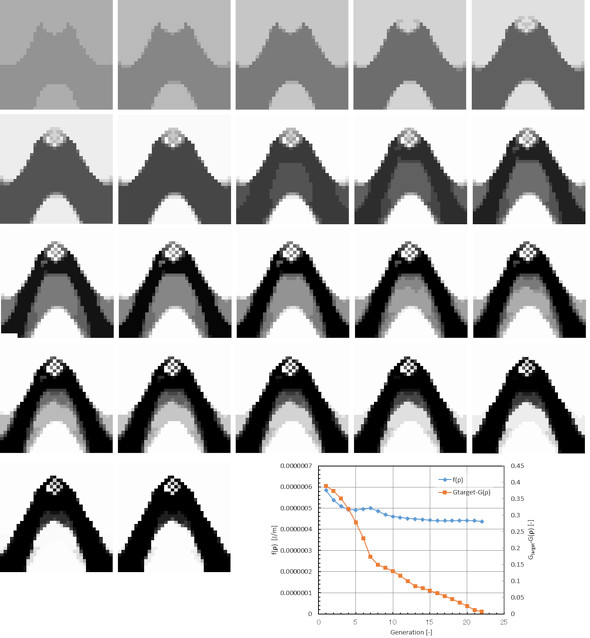
　では、同じことを「トポロジー最適化」で行ってみましょう。解析モデルを図21に、トポロジー最適化の過程を図22に示します。図22の右下のグラフの青色プロットはひずみエネルギーで、ひずみエネルギーが極小値に向かって変化しています。オレンジ色のブロットは、重力制御関数Gと重力制御関数の目標値G_target（0.95）との差で、第22世代で目標値に到達しています。

図21　トポロジー最適化の解析境界条件［クリックで拡大］

図22　トポロジー最適化の過程［クリックで拡大］

　では、領域最適化とトポロジー最適化の結果を比較しましょう。両者を重ね合わせたものを図23に示します。そこそこ一致しています。ひずみエネルギー最小化（平均コンプライアンス最小化）を目標として、全く異なるアプローチでここまで一致したことに注目したいと思います。お互いが相手の有効性を裏付けているのではと考えています。