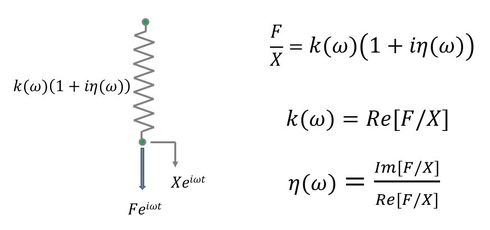ランドリー(洗濯機)を題材に音振動の低次元化モデリングを考える:1Dモデリングの勘所(8)(2/3 ページ)
振動数が変化する外力のモデリング
外力の振動数が一様に変化する場合の表現方法について考える。“外力の振動数が一様に変化する”とは、「角加速度が一定値である」ということなので、位相をΦとすると、角加速度は、
と表現できる。ここに+のとき「昇速」、−のとき「減速」となり、εは昇降速の速さを表現する正の定数である。上式から、外力の角振動数および位相は、
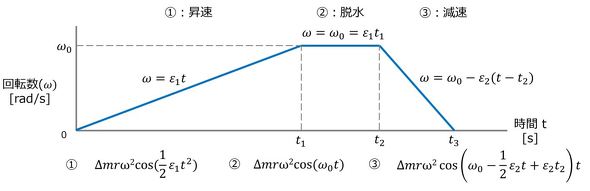
となる。ここに、ωは初期状態の角振動数、αは位相角である。上記の知見を基に、脱水時回転槽の回転数変化を表現すると図6となる。すなわち、静止状態から、角加速度ε1、角速度ε1tで昇速、所定の回転数ω0で脱水、その後、角加速度−ε2、角速度ω0−ε2(t−t2)で減速する。ここで、時刻0からt1までが昇速、t1からt2までが一定回転、t2からt3までが減速区間である。各区間の外力は図6下部に示すように表現される。
粘弾性体(ゴム)のモデリング
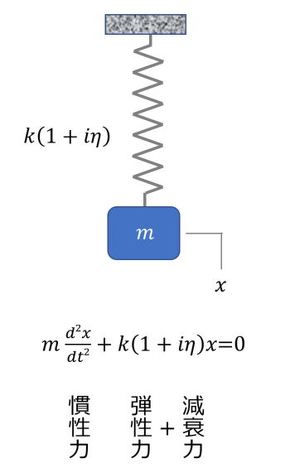
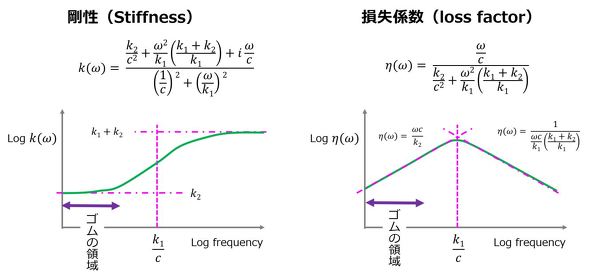
ゴムは、防振材料として使用されることが多い。これは良好な減衰特性を有するためであるが、一方で通常の金属材料とは異なり、モデリングが容易ではなく、さまざまな試みが行われている。すなわち、ゴムはいわゆる粘弾性体で、材料自体が剛性と減衰特性を有する。そこで、一般には図7に示すように複素数剛性で表現される。ここで、kが剛性に関するもので、ηが損失係数と呼ばれ、減衰に関するものである。また、粘弾性ばねの場合には、剛性も損失係数も周波数ωの関数となるため、図8のように定義される。
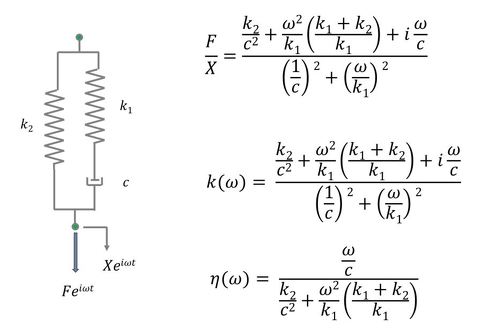
粘弾性ばねのモデリング方法として、ばね要素と減衰要素を組み合わせた図9の粘弾性ばねモデルが使用される。このように、2種類のばね要素、減衰要素、振動数を用いて、剛性と損失係数を表現できる。図9の剛性と損失係数を横軸に、振動数をとって示すと図10のようになる。実験などにより、ゴム材料の剛性、損失係数を把握し、これを表現するように2種類のばね要素と減衰要素の値を定義することになる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 共振はなぜ起きる? ばね−マス系と伝達関数で考える
- なぜ「最新の優れた技術」が現場で使われないのか
- 「MacBook Neo」は財布だけでなく、環境にも優しい
- 設計者の思考を止めないという視点
- 3Dプリンタ用高靭性材料「ToughONE」の対応機種を小型モデルへ拡大
- 【レベル4】図面の穴寸法の表記を攻略せよ!
- 主応力とミーゼス応力は何が違うのか 「応力」で考える強度設計の基本
- ダイモンの超小型月面探査車「YAOKI」、発明大賞の本賞を受賞
- キヤノン、32年連続でiF DESIGN AWARDを受賞 金賞に全身用X線CT診断装置が選出
- 変形玩具から着想のICOMA「TATAMEL BIKE」がiF DESIGN AWARD 2026を受賞
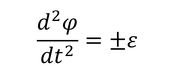 式1
式1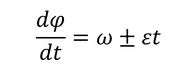 式2
式2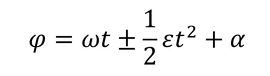 式3
式3